Question 1183372: Each ordered pair (t, N) represents the year t and the number N (in thousands) of female participants in high school athletic programs during 13 school years, with t = 1 corresponding to the 2000 - 2001 school year.
(1, 2783), (2, 2809), (3, 2852), (4, 2865), (5, 2907), (6, 2954), (7, 3020)(8,3055), (9, 3111), (10, 3172), (11, 3175), (12, 3225), (13, 3235)
Use the regression feature in your graphing calculator to find the following models and their coefficient of determination. Round to 4 decimal places.
a.Linear Model:𝑁(𝑡)=2723.5385+41.2857t
𝑟2=0.9873
Exponential Model:𝑁(𝑡)= (2732.9970)(1.0138)^t
𝑟2= 0.9874
Power Model:𝑁(𝑡)= 2685.2908t^0.0655
𝑟2= 0.8696
(d)Which model best fits the data? Explain.
(e)Use the model you chose in part (d) to predict the school year in which about 3,727,000 girls will participate.
Answer by ikleyn(52869)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hello, in this post, I see three regression models, written without explanations about their origins.
OK, I will suppose that you (or somebody else) produced these models, and I will not check if they are correct.
Question (d) asks which model is better.
Near to each model, I see the parameter r^2 (with no explanations on its meaning).
Usually, in such problems, r^2 denotes the calculated sum of quadratic point-to-point deviations of the points from the regression.
If so, then the best regression is where r^2 is minimal.
So, the Power Model looks like the best.
Regarding part (e), write this equation for the Power Model
2685.2908t^0.0655 = 3727,
take logarithm base 10 of both sides
log(2685) + 0.0655*log(t) = log(3727)
express and calculate log(t)
log(t) =  = 2.17
and restore t
t = = 2.17
and restore t
t = 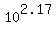 = 148 years.
So, the prediction is 148 years after 2000.
Honestly, this result seems to be strange to me, but i got it formally from your data.
I have serious suspitions, that either the problem is defective, or your data related to the regression is incorrect.
But it is just the material for you to search for the truth. = 148 years.
So, the prediction is 148 years after 2000.
Honestly, this result seems to be strange to me, but i got it formally from your data.
I have serious suspitions, that either the problem is defective, or your data related to the regression is incorrect.
But it is just the material for you to search for the truth.
|
|
|