Question 1183317: At 3:00 PM, Andy began walking directly south from point A at a rate of 4 mi/h. At the same time, Bill started walking directly west from point B to point A, at a rate of 5 mi/h. The distance between A and B is 9 miles. Assume that both of them stop walking when Bill reaches point A.
At what time will be distance between Andy and Bill be minimized?
Round your answer to the nearest minute.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
At 3:00 PM, Andy began walking directly south from point A at a rate of 4 mi/h.
At the same time, Bill started walking directly west from point B to point A, at a rate of 5 mi/h.
The distance between A and B is 9 miles. Assume that both of them stop walking when Bill reaches point A.
At what time will be distance between Andy and Bill be minimized?
Round your answer to the nearest minute.
~~~~~~~~~~~~~~
Place the origin of the coordinate system at the point A.
Then the point B has coordinates (9,0), from the context.
At time "t" hours after 3:00 PM, Andy's location is the point (0,-4t),
while Bill's location is the point (9-5t,0).
The square of the distance between Andy and Bill, as the function of time, is
d^2(t) =  + + 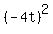 = = 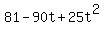 + +  = = 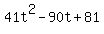 .
The distance between the persons is minimal when the SQUARE of the distance is minimal.
Thus, to find the time of the minimal distance between the persons, it is enough to differentiate the function d^2(t)
over t and equate it to zero. It gives the equation
2*41*t - 90 = 0, or 82t = 90, t = .
The distance between the persons is minimal when the SQUARE of the distance is minimal.
Thus, to find the time of the minimal distance between the persons, it is enough to differentiate the function d^2(t)
over t and equate it to zero. It gives the equation
2*41*t - 90 = 0, or 82t = 90, t = 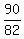 hours = 1.097561 hours = 1 hour and 6 minutes (rounded to the nearest minute, as requested).
ANSWER. The distance between the persons is minimal at t = 1 hour and 6 minutes after 3:00 PM, i.e. at 4:06 PM. hours = 1.097561 hours = 1 hour and 6 minutes (rounded to the nearest minute, as requested).
ANSWER. The distance between the persons is minimal at t = 1 hour and 6 minutes after 3:00 PM, i.e. at 4:06 PM.
Solved.
Below are the plots of the square of the distance 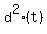 and the distance itself and the distance itself 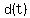 as functions of time "t". as functions of time "t".
 Plots d^2(t) =
Plots d^2(t) = 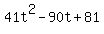 (red) and d(t) = (red) and d(t) = 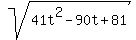 (green) (green)
|
|
|