SOLUTION: A polygon has two interior angles of 120 degrees each and the others are 150 degrees.Calculate a. The number of sides of the polygon b. The sum of interior angles

Click here to see ALL problems on Polygons

Question 1183295: A polygon has two interior angles of 120 degrees each and the others are 150 degrees.Calculate a. The number of sides of the polygon b. The sum of interior angles
Found 3 solutions by Plocharczyk, ikleyn, MathTherapy:
Answer by Plocharczyk(17)   (Show Source):
You can put this solution on YOUR website!
A polygon has two interior angles of 120 degrees each and the others are 150 degrees.
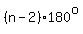240 + 150m = (n-2)180 where n = the number of sides and m = the number of 150° angles. The number of sides could be 5, then there would be 2 120^o interior angles, and 2 150° angles. The sum would be 540^o. The number of sides could be 10, then there would be 2 120^o interior angles, and 8 150° angles. The sum would be 1440^o. The number of sides could be 15, then there would be 2 120^o interior angles, and 14 150° angles. The sum would be 2340^o. The number of sides could be 20, then there would be 2 120^o interior angles, and 20 150° angles. The sum would be 3240^o. The number of sides could be 25, then there would be 2 120^o interior angles, and 26 150° angles. The sum would be 4140^o. The number of sides could be 30, then there would be 2 120^o interior angles, and 32 150° angles. The sum would be 5040^o. This list could go on and on forever. Edwin

Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website!
.

Let "n" be the number of sides of the polygon (the same as the number of vertices). Two interior angles are 120 degrees each, and the other (the rest) (n-2) interior angles are 150 degrees each. Write equation for the sum of all interior angles 120 + 120 + (n-2)*150 = (n-2)*180. Simplify and find "n" 240 + 150n - 300 = 180n - 360 240 + 360 - 300 = 180n - 150n 300 = 30n n = 300/30 = 10. Thus the polygon has 10 sides and 10 vertices. The sum of the interior angles is (10-2)*180 = 8*180 = 1440 degrees. ANSWER

Solved.

Answer by MathTherapy(10557)   (Show Source):
You can put this solution on YOUR website!
A polygon has two interior angles of 120 degrees each and the others are 150 degrees.Calculate a. The number of sides of the polygon b. The sum of interior angles

Since 2 interior angles measure 120^o each, then 2 exterior angles measure 180^o - 120^o = 60^o each Let number of angles (exterior/interior), be n With 2 angles known, remaining angles = n - 2 Since remaining interior angles measure 150^o each, remaining exterior angles measure 180^o - 150^o = 30^o each. So, remaining exterior angles measure a total of 30(n - 2) = 30n - 60 With all exterior angles measuring 120^o and (30n - 60)^o, and since the exterior angles of any polygon sum to 360^o, we now have: 120 + 30n - 60 = 360 60 + 30n = 360 30n = 300 Number of sides, or Sum of interior angles: OR Two (2) interior angles measure 120^o each, so 2 interior angles measure 2(120)^o Let number of angles (exterior/interior), be n With 2 interior angles known, remaining angles = n - 2 Since remaining interior angles measure 150^o each, remaining interior angles measure 180(n - 2)^o With all interior angles measuring 2(120)^o and 150(n - 2)^o, and since the interior angles of any polygon sum to 180(n - 2)^o, we now have: 2(120) + 150(n - 2) = 180(n - 2) 240 = 180(n - 2) - 150(n - 2) 240 = 30(n - 2) Number of sides, or Sum of interior angles: