Question 1183251: Outside temperature over a day can be modelled as a sinusoidal function. Suppose you know the high temperature for the day is 90 degrees and the low temperature of 80 degrees occurs at 6 AM. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.
D(t)=
How do i go about this question
Found 3 solutions by Theo, ikleyn, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! in a 24 hour day, the low is 80 degrees and the high is 90 degrees.
the low occurs at 6:00 am.
you don't say when the high occurs, however, if it is modeled by a sinusoidal function, it would have to be either sine or cosine.
tangent won't do because tangent doesn't have a low or a high, i.e. the low or high in the tangent function is plus or minus infinity.
i'll use sine function.
we want the period to be 24 hours.
that makes the frequency equal to 360 / 24 = 15.
the general form is y = a * sin(b * (x - c)) + d
a is the amplitude.
b is the frequency.
c is the horizontal shift.
d is the vertical shift.
the amplitude will be plus or minus 5 from the horizontal center line.
the vertical shift will make the horizontal center line 85 units above the x-axis.
so far, the equation looks like it will be:
y = 5 * sin(15 * (x-c)) + 85.
with a 0 horizontal shift, the equation becomes:
y = 5 * sin(15 * (x - 0)) + 85.
that looks like this:

i saw that, if i made the amplitude -5 instead of +5, that the low point would be at 6:00 am.
the equation would be y = -5 * sin(15 * (x - 0)) + 85.
that looks like this:

i then saw that, if i left the amplitude as +5, but shifted the graph to the left 12 units, that i would also get the low point at 6:00 am.
that equation would be y = 5 * sin(15 * (x + 12)) + 85.
that looks like this:

i could also have used the cosine function.
it give the same graph, with the same amplitude and frequency and vertical shift, but the horizontal shift would have to be different.
one possible equation would be:
y = -5 * cos(15 * (x - 6)) + 85
that looks like this:

Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Outside temperature over a day can be modelled as a sinusoidal function.
Suppose you know the high temperature for the day is 90 degrees and the low temperature of 80 degrees occurs at 6 AM.
Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.
D(t)=
How do i go about this question
~~~~~~~~~~~~~~~~
The difference between the highest and lowest temperature is 90 - 80 = 10 degrees;
hence, the midline is 85 degrees and the amplitude is  = 5 degrees.
Next, if x is the time starting from 6 am (x= 0 when the temperature is lowest), then OBVIOUSLY, the temperature as a function of x is
D(x) = = 5 degrees.
Next, if x is the time starting from 6 am (x= 0 when the temperature is lowest), then OBVIOUSLY, the temperature as a function of x is
D(x) = 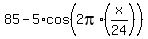 (1)
(we use the sign " - " to reflect cosinusoid about the midline, and we use the ratio x/24 to model the period of 24 hours).
Now, if t is the time after midnight, then x = t-6, so the formula (1) takes the final form
D(t) = (1)
(we use the sign " - " to reflect cosinusoid about the midline, and we use the ratio x/24 to model the period of 24 hours).
Now, if t is the time after midnight, then x = t-6, so the formula (1) takes the final form
D(t) = 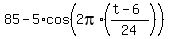 . ANSWER
Or, if you like to use degrees instead of radians, then the same formula takes an EQUIVALENT form
D(t) = . ANSWER
Or, if you like to use degrees instead of radians, then the same formula takes an EQUIVALENT form
D(t) = 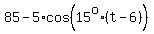 . ANSWER . ANSWER
Solved.
=============
How tutor @Theo solved the problem, is a formal presentation; but as far as I know, in reality,
nobody solves such problems in this way, and (in my opinion) it is not a good way to teach students.
I am 100% convinced that after such teaching, although formally it is right, the students' understanding will be ZERO.
What I showed you in my post, is a way to solve such problems using common sense
(combined with the knowledge of elementary Trigonometry). I hope, it is much more educative.
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|