SOLUTION: Hello, this is a mathematical induction question i had a hard time to prove Show that, for every positive integer n: a 1^2 + 3^2 + 5^2 + … + (2n − 1)^2 = (n(4n^2 - 1))/3

Algebra ->  Sequences-and-series -> SOLUTION: Hello, this is a mathematical induction question i had a hard time to prove Show that, for every positive integer n: a 1^2 + 3^2 + 5^2 + … + (2n − 1)^2 = (n(4n^2 - 1))/3      Log On


   

Question 1183221: Hello, this is a mathematical induction question i had a hard time to prove
Show that, for every positive integer n:
a 1^2 + 3^2 + 5^2 + … + (2n − 1)^2 = (n(4n^2 - 1))/3
Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!


LHS is  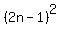1%5E2%2B3%5E2+...++%282n-1%29%5E2+      (1)

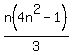RHS is  n%284n%5E2-1%29%2F3                   (2)





Base case:

n=1:   LHS is 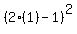+%282%281%29-1%29%5E2+ = 1

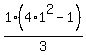       RHS is +1%2A%284%2A1%5E2-1%29%2F3+ = (4-1)/3 }}} = 1 



Base case holds.



Hypothesis:

       Assume LHS = RHS for  n=k             (*)





Step case: 

        Let n=k+1  (recall the index k counts by 1 and the 2k-1 in the LHS & RHS is what makes sure you have odd numbers only)



What you need to do now, is show LHS=RHS for n=k+1, then the proof is complete.



LHS is 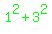 +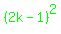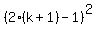green%28+1%5E2%2B3%5E2+%29++...++green%28%282k-1%29%5E2%29+ + +%282%28k%2B1%29-1%29%5E2+ 

Where I have separated the (k+1)th term.  The terms in green are the n=k case, which by the hypothesis (*), can be replaced by 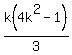k%284k%5E2-1%29%2F3, giving:



LHS = 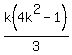+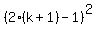k%284k%5E2-1%29%2F3+ + +%282%28k%2B1%29-1%29%5E2+



    ...expand and simplify... 

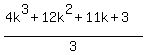
    = +%284k%5E3%2B12k%5E2%2B11k%2B3%29%2F3+



    ... factor (I used WolframAlpha, you could also guess k+1 as likely

factor and do the division)...



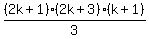
    = +%282k%2B1%29%282k%2B3%29%28k%2B1%29+%2F+3+

  

Is this last expression the same as (2)?

  Let u=k+1,  --> k=u-1

  Then the last expression above, in terms of u, is:

     = +%282%28u-1%29%2B1%29%282%28u-1%29%2B3%29u%29%2F3+

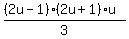
     = +%28%282u-1%29%282u%2B1%29u%29%2F3+

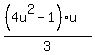     = ++%28%284u%5E2-1%29u%29%2F3+   Yes, it is the same (replace u with n).  Proof complete.