Question 1183213: A bag contains 10 red marbles, 8 white marbles, and 8 blue marbles. You draw 5 marbles out at random, without replacement. What is the probability that all the marbles are red?
The probability that all the marbles are red is
This question I can solve, P(5xred) = (10/36)*(9/35)*(8/34)*(7/33)*(6/32) = 1/1496
What is the probability that exactly two of the marbles are red?
The probability that exactly two of the marbles are red is
I can't seem to get this one right. I assumed it just was (10/36)*(9/35) but that is not the case. I know that the "exactly" part is important I just don't know what to do in that case.
What is the probability that none of the marbles are red?
The probability of picking no red marbles is
This to be similar to the complement of the first question, but that does not give th right answer, I tried 1-((10/36)*(9/35)*(8/34)*(7/33)*(6/32)) which is incorrect. I have tried (16/36)*(15/35)*(14/34)*(13/33)*(12/32) but this is also incorrect. So I am stuck. I don't know what to do anymore.
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A bag contains 10 red marbles, 8 white marbles, and 8 blue marbles. You draw 5 marbles out at random, without replacement.
(1) What is the probability that all the marbles are red?
The probability that all the marbles are red is
This question I can solve, P(5xred) = (10/36)*(9/35)*(8/34)*(7/33)*(6/32) = 1/1496
(2) What is the probability that exactly two of the marbles are red?
The probability that exactly two of the marbles are red is
I can't seem to get this one right. I assumed it just was (10/36)*(9/35) but that is not the case.
I know that the "exactly" part is important I just don't know what to do in that case.
(3) What is the probability that none of the marbles are red?
The probability of picking no red marbles is
This to be similar to the complement of the first question, but that does not give th right answer,
I tried 1-((10/36)*(9/35)*(8/34)*(7/33)*(6/32)) which is incorrect. I have tried (16/36)*(15/35)*(14/34)*(13/33)*(12/32)
but this is also incorrect. So I am stuck. I don't know what to do anymore.
~~~~~~~~~~~~~~~~~~~~~~
(1) You INCORRECTLY calculated the answer to this question.
The correct formula is P = (10/26)*(9/25)*(8/24)*(7/23)*(6/22) = 0.003831 (approx.; rounded). ANSWER
(2) In this case, the probability is THIS FRACTION
P = 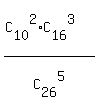 .
The denominator .
The denominator 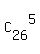 is the number of all combinations of 26 marbles taken 5 at a time.
In other words, it is the number of all possible 5-marble subsets of the given set of 26 marbles.
It is so called "the set of all possible events" in this problem. is the number of all combinations of 26 marbles taken 5 at a time.
In other words, it is the number of all possible 5-marble subsets of the given set of 26 marbles.
It is so called "the set of all possible events" in this problem.
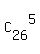 = =  = 65780.
The numerator in the formula is the number of all possible 5-marble subsets, containing EXACTLY 2 red marbles.
This number is = 65780.
The numerator in the formula is the number of all possible 5-marble subsets, containing EXACTLY 2 red marbles.
This number is  . .  = 45 * 560 = 25200.
THEREFORE, the final probability in this case is P = = 45 * 560 = 25200.
THEREFORE, the final probability in this case is P = 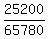 = 0.3831 (approx.; rounded). ANSWER
(3) In this case, you select from 16 non-red marbles; so the probability is
P = (16/26)*(15/25)*(14/24)*(13/23)*(12/22) = 0.0664 (approx.; rounded). ANSWER = 0.3831 (approx.; rounded). ANSWER
(3) In this case, you select from 16 non-red marbles; so the probability is
P = (16/26)*(15/25)*(14/24)*(13/23)*(12/22) = 0.0664 (approx.; rounded). ANSWER
Solved.
All questions are answered and carefully explained.
|
|
|