SOLUTION: 525 tickets were sold for a game for a total of $987.50. If adult tickets sold for $2.50 and children's tickets sold for $1.50, how many of each kind of ticket were sold?

Algebra ->  Coordinate Systems and Linear Equations  -> Linear Equations and Systems Word Problems -> SOLUTION: 525 tickets were sold for a game for a total of $987.50. If adult tickets sold for $2.50 and children's tickets sold for $1.50, how many of each kind of ticket were sold?      Log On


   

Question 1183208: 525 tickets were sold for a game for a total of $987.50. If adult tickets sold for $2.50 and children's tickets sold for $1.50, how many of each kind of ticket were sold?
Answer by ikleyn(52767) About Me  (Show Source):
You can put this solution on YOUR website!
.
525 tickets were sold for a game for a total of $987.50. If adult tickets sold for $2.50
and children's tickets sold for $1.50, how many of each kind of ticket were sold?
~~~~~~~~~~~~~~~ 

x  adult tickets, and

(525-x) children's tickets.


Write the total money (revenue) equation


    2.50x + 1.50(525-x) = 987.50   dollars.


From the equation


    x = 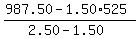%28987.50-1.50%2A525%29%2F%282.50-1.50%29 = 200.


ANSWER.  200 adult tickets and 525-200 = 325 children tickets.


CHECK.  2.50*200 + 1.50*325 = 987.50  dollars, in total.    ! Correct !

Solved.