.
Prove that there are infinitely many natural numbers n such that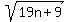 
is irrational.
~~~~~~~~~~~~~~~
The proof is very simple.
I'd say, it is UNEXPETEDLY simple.
Consider any integer positive number " n ", which has the last digit of 2.
(In other words, consider any integer positive number n such that n = 2 (mod 10) ).
For example, such numbers "n" are 12, 22, 32, 42, 52 . . . and so on.
Then the number 19n has the last digit of 8, and the number (19n+9) has the last digit of 7, because 8 + 9 = 17 = 7 (mod 10).
+-------------------------------------------------------------------------+
| But NO ONE such integer positive number is a perfect square (!) |
+-------------------------------------------------------------------------+
(Notice that a square of an integer number may have the last digit only 0, 1, 4, 5, 6, 9, but may not have the last digit of 2, 3, 7, 8).
Therefore, all the numbers (19n +9) with n = 2 (mod 10) are not perfect squares and, THEREFORE, create/produce IRRATIONAL numbers .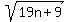
PROVED.
and Solved.
