Question 1182908: Given that f : x maps to ax + b and f^3 : x maps to 27x + 26, Find the value of a and of b, Find an expression for f^4
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52900)   (Show Source):
You can put this solution on YOUR website! .
Given that f : x maps to ax + b and f^3 : x maps to 27x + 26,
Find the value of a and of b, Find an expression for f^4
~~~~~~~~~~~~~~~
f^2(x) = a*(ax+b) + b = (a^2)x + ab + b.
f^3(x) = (a^2)*(ax+b) + ab + b = (a^3)x + (a^2)*b + ab + b = 27x + 26.
From the last equation, a^3 = 27; hence, a = 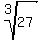 = 3.
Then we have
3^2*b + 3b + b = 26, or 9b + 3b + b = 26, 13b = 26, b = 26/13 = 2.
So, f(x) = 3x + 2.
Finally, f^4(x) = 27(3x+2) + 26 = 81x + 54 + 26 = 81x + 80. <<<---=== I just edited this line after the notice by @robertb. Thanks (!)
ANSWER. a= 3; b= 2; f^4(x) = 81x + 80.
Solved.
Answer by robertb(5830)  (Show Source):
You can put this solution on YOUR website! Ikleyn's solution is correct, except for the last line, where it should read
f^4(x) = 27(3x+2) + 26 = 81x + 54 + 26 = 81x + 80.
|
|
|
