SOLUTION: A baker purchased 13 lb of wheat flour and 10 lb of rye flour for a total cost of $14.10. A second purchase, at the same prices, included 15 lb of wheat flour and 14 lb of rye flou

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: A baker purchased 13 lb of wheat flour and 10 lb of rye flour for a total cost of $14.10. A second purchase, at the same prices, included 15 lb of wheat flour and 14 lb of rye flou      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1182899: A baker purchased 13 lb of wheat flour and 10 lb of rye flour for a total cost of $14.10. A second purchase, at the same prices, included 15 lb of wheat flour and 14 lb of rye flour. The cost of the second purchase was $17.50. Find the cost per pound of the wheat flour and of the rye flour.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39623) About Me  (Show Source):
You can put this solution on YOUR website!
too common an application for two-variable linear equations system
so many like this already been solved

w Wheat Flour price
r Rye Flour price

system%2813w%2B10r=14.1%2C15w%2B14r=17.5%29
What method do you want to use?


system%287%2813w%2B10r%29=7%2A14.1%2C5%2815w%2B14r%29=5%2A17.5%29--------if you continue with this, you will be able to eliminate terms of r, and first solve for w.
.
.

Answer by ikleyn(52834) About Me  (Show Source):
You can put this solution on YOUR website!
.
A baker purchased 13 lb of wheat flour and 10 lb of rye flour for a total cost of $14.10.
A second purchase, at the same prices, included 15 lb of wheat flour and 14 lb of rye flour.
The cost of the second purchase was $17.50.
Find the cost per pound of the wheat flour and of the rye flour.
~~~~~~~~~~~~~~ 

Let  x  be the price per pound of the wheat and 

let  y  be the price per pound of the rye flour.


Write the system of two equations as you read the problem


    13x + 10y = 14.10    (1)

    15x + 14y = 17.50    (2)



Use the determinant method to solve the system (the same as the Cramer's rule).



The determinant of the coefficient matrix is  D = 13*14 - 15*10 = 32.



The determinant to find the unknown x is      Dx = 14.10*14 - 17.50*10 = 22.4;

    so  x = 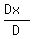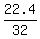%28Dx%29%2FD = 22.4%2F32 = 0.7  dollars.



The determinant to find the unknown y is      Dy = 13*17.50 - 15*14.10 = 16;

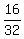    so  y = Dy%2FD = 16%2F32 = 0.5  dollars.


ANSWER.  The prices are  $0.7  for pound of wheat and  $0.5 for pound of rye flour.

Solved.

-----------------

On Cramer's rule for solving systems of 2 equations in 2 unknowns see the lessons
    - What is a matrix?,
    - Determinant of a 2x2-matrix,
    - HOW TO solve system of linear equations in two unknowns using determinant (Cramer's rule),
    - Solving systems of linear equations in two unknowns using the Cramer's rule,
    - Solving word problems by the Cramer's rule after reducing to systems of linear equations in two unknowns,
in this site.

Also, you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic
     "2x2-Matrices, determinants, Cramer's rule for systems in two unknowns"