Question 1182840: Evaluate the following inverse trigonometric function.
1. sin^-1(-1)
2. tan^-1(-1)
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52894)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. sin^-1(-1) = 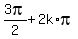 , k = any integer number = 0, +/- 1, +/- 2, . . . ANSWER
2. tan^-1(-1) = , k = any integer number = 0, +/- 1, +/- 2, . . . ANSWER
2. tan^-1(-1) = 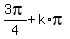 , k = any integer number = 0, +/- 1, +/- 2, . . . ANSWER , k = any integer number = 0, +/- 1, +/- 2, . . . ANSWER
Solved and answered.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Evaluate the following inverse trigonometric function.
1. sin^-1(-1)
2. tan^-1(-1)
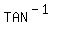   
asks the question "What angle between -90o and 90o has a tangent of -1?"
Since its tangent is negative, and we know that the tangent is negative in
QII and QIV, the angle must be in QIV because QII is not between -90o and 90o.
We also know that since the tangent is the opposite/adjacent, that to have
absolute value 1, the opposite and the adjacent sides must be equal in
length (absolute value). How can that be? It's when we have an isosceles
right triangle, with equal opposite and adjacent sides, which is a 45o-45o-90o
right triangle in QIV, like this:
 So
So 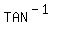   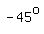  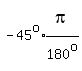  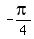 ---------------------------------------------------------------------
---------------------------------------------------------------------
    asks the question "What angle between -90o and 90o has a sine of -1?"
Since its sine is negative, and we know that the sine is negative in QIII and QIV.
We also know that since the sine is the opposite/hypotenuse, that to have
absolute value 1, the opposite and the hypotenuse must be equal in absolute
value. How can that be? It's when the right triangle has been "squashed"
into a line segment on the y-axis between QIII and QIV, like the heavy
line below. The adjacent side has been "squashed" down to 0, just a point.
asks the question "What angle between -90o and 90o has a sine of -1?"
Since its sine is negative, and we know that the sine is negative in QIII and QIV.
We also know that since the sine is the opposite/hypotenuse, that to have
absolute value 1, the opposite and the hypotenuse must be equal in absolute
value. How can that be? It's when the right triangle has been "squashed"
into a line segment on the y-axis between QIII and QIV, like the heavy
line below. The adjacent side has been "squashed" down to 0, just a point.

   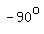  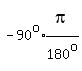   BOTH ANGLES ABOVE ARE NEGATIVE BECAUSE THEY BOTH ROTATE CLOCKWISE FROM THE
RIGHT SIDE OF THE x-AXIS.
Edwin
BOTH ANGLES ABOVE ARE NEGATIVE BECAUSE THEY BOTH ROTATE CLOCKWISE FROM THE
RIGHT SIDE OF THE x-AXIS.
Edwin
|
|
|