Question 1182824: A block is started from rest at the top of an inclined plane 6 meters long which makes 45 degrees with the horizontal. The coefficient of friction between the block and the plane is 0.20. At the foot of the plane, the block continues to move along a horizontal surface. If the coefficient of friction between the block and the horizontal surface is 0.15, how far does the block go along the horizontal surface?
Answer by ikleyn(52769)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A block is started from rest at the top of an inclined plane 6 meters long which makes 45 degrees with the horizontal.
The coefficient of friction between the block and the plane is 0.20. At the foot of the plane, the block continues
to move along a horizontal surface. If the coefficient of friction between the block and the horizontal surface is 0.15,
how far does the block go along the horizontal surface?
~~~~~~~~~~~~~
The idea of the solution is to calculate the potential energy of the block at the top of the inclined plane;
then subtract from it the amount of energy, which the block loses due to friction, while it moves from the top to the bottom;
and finally find the distance moving along the horizontal surface by equating the rest of the energy to the work
of the friction force.
So, below I realize/implement this program step by step.
(1) The potential energy P of the block at the top of the inclined plane is P = mgh =  = = 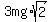 joules.
Here m is the mass of the block and g is the gravity acceleration.
(2) On the inclined plane surface, the normal reaction force N is N = joules.
Here m is the mass of the block and g is the gravity acceleration.
(2) On the inclined plane surface, the normal reaction force N is N = 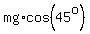 = =  newtons;
therefore, the friction force newtons;
therefore, the friction force 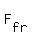 is is 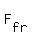 = = 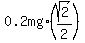 newtons
and the work done by this friction force is newtons
and the work done by this friction force is 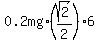 = = 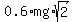 joules.
Hence, the energy of the block, when it reaches the bottom of the inclined plane is the difference joules.
Hence, the energy of the block, when it reaches the bottom of the inclined plane is the difference
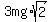 - - 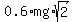 = = 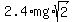 joules.
(3) On the horizontal plane, the weight of the box is mg newtons and the friction force is 0.15*mg newtons.
If "d" is the unknown traveled distance along the horizontal plane, then the work of the friction force is 0.15*mg*d joules.
To find the distance d, we equate this energy to the energy of the block at the bottom of the inclined plane, which we found in part (2).
We get the equation then
0.15*mg*d = joules.
(3) On the horizontal plane, the weight of the box is mg newtons and the friction force is 0.15*mg newtons.
If "d" is the unknown traveled distance along the horizontal plane, then the work of the friction force is 0.15*mg*d joules.
To find the distance d, we equate this energy to the energy of the block at the bottom of the inclined plane, which we found in part (2).
We get the equation then
0.15*mg*d = 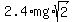 .
Cancel the factor mg in both sides and find d
d = .
Cancel the factor mg in both sides and find d
d = 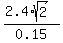 = 22.627 meters. ANSWER = 22.627 meters. ANSWER
The problem is just solved, and the solution is carefully presented with all accompanied explanations.
Happy learning (!)
|
|
|