.
Pauline Wong spends three hours selling a used car and five hours selling a new car she works no more than 31 hours per week.
In order to receive a bonus she must sell at least two used cars and two new cars each week.
In that case she receives a bonus of 200 for each used car and 300 for each new car.
How many cars and how many used cars can she try to sell to maximize her bonus? what is the maximum bonus?
a. define the variables to use
b. goal function
c. constraints
e. optimal solution
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let U be the number of USED cars sold, and
let N be the number of NEW cars sold.
Then the goal function is
Maximize bonus function, which is defined this way
B(U,N) = 200U + 300N, if both U >= 2, N >= 2 and B(U,N) = 0 otherwise (1)
under THESE CONSTRAINS
3U + 5N <= 31. (2)
It remainds linear programming problem, but it has two features, that make it very special and different
from standard linear minimax problems. These differences are:
- the problem is actually NON-linear, sinse the definition (1) is non-linear,
and
- the solution should be in integer numbers U and N, i.e., the solution is among the points of the integer grid
in the first quadrant satisfying (2)
Due to these features, the standard linear programming method DOES NOT WORK in this problem.
So, we should think on how to solve it.
First, it is OBVIOUS, that the non-linear condition (1) can be simplified.
For a moment, we can forget about this requirement "if both U >= 2, N >= 2 and B(U,N) = 0 otherwise" and simply OMIT it;
so the object function will be B(U,N) = 200U + 300N.
Second, it is clear, that we should look for the solution not for all integer (U,N) satisfying (2):
it is enough for each integer U between 0 and 10 to consider the MAXIMAL integer N satisfying (2).
Thus the algorithm becomes clear and simple:
- for eleven integer numbers U from 0 to 10 inclusive, calculate maximal integer N satisfying (2);
- for every such pair (U,N) calculate the bonus function B(U,N) = 3U + 5N.
- exclude those pairs (U,N) and values B(U,N), where U < 2 or N < 2;
- among the rest of values B(U,N) select the maximum value B(U,N);
- then the corresponding values of U and N provide the solution.
This algorithm can be easily realized and executed even manually;
but I used MS Excel in my computer to facilitate this task.
The results are in the Table below:
T A B L E
U N_real N B(U,N)
----------------------------------------
0 6.2 6 1800 -
1 5.6 5 1700 -
2 5 5 1900 +
3 4.4 4 1800 +
4 3.8 3 1700 +
5 3.2 3 1900 +
6 2.6 2 1800 +
7 2 2 2000 + (*)
8 1.4 1 1900 +
9 0.8 0 1800 -
10 0.2 0 2000 -
The column N_real is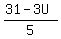 
; the next column N is the closest lesser or equal integer to it.
In the last column, the "-" sign marks "defective" lines, where the condition (1) is violated;
these lines should be corrected, and the values of B(U,N) should be replaced by 0 (zero) in these lines.
The rest lines are marked by "+".
So, the ANSWER is THIS:
the optimum solution is the pair (N,U) = (7,2) : 7 used cars and 2 new cars, giving the maximum bonus of 2000.
It is marked (*) in the Table.
Solved.
