|
Question 1182583: The point P has coordinates (a,b). Another point Q is formed by reversing the coordinates of P, i.e. Q has coordinates (b,a).
(i) Show that PQ is perpendicular to the line y=x.
(ii) Show that the midpoint, M, of PQ lies on y=x.
Answer by ikleyn(52794)   (Show Source):
You can put this solution on YOUR website! .
The point P has coordinates (a,b). Another point Q is formed by reversing the coordinates of P,
i.e. Q has coordinates (b,a).
(i) Show that PQ is perpendicular to the line y=x.
(ii) Show that the midpoint, M, of PQ lies on y=x.
~~~~~~~~~~~~~~~~~~~
In this problem, it is assumed that a =/= b --- otherwise, the statement loses sense.
So, I will assume that a =/= b, although the problem does not says it explicitly.
Part ( i )
Let's compare slopes of the line y = x and the line (segment) PQ.
The line y = x has the slope equal to 1, OBVIOUSLY.
The segment PQ hs the slope m = 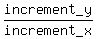 =  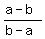= -1.
The slopes 1 and -1 are negatively reciprocal: 1*(-1) = -1; THEREFORE, the line y = x and the segment (the line) PQ are perpendicular.
Thus the first statement is proved.
Part ( ii )
The coordinates of the midpoint are ( ,).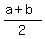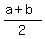
Both x- and y- coordinates are equal.
It proves, that the midpoint lies on the line y = x.
Thus the second statement is proved, too.
///////////
The points P and Q are mirror reflections each other about the line y = x.
|
|
|
| |
