.
Find the probability that a single toss of a die will result in a number less than 4
if it is given that the toss resulted in an odd number.
~~~~~~~~~~~~~~
It is the CONDITIONAL probability problem.
There are two major ways to solve it, and I will show you BOTH ways.
The full space of events consists of 6 events getting "1", '2", "3", "4", "5" and "6".
The probability for each event is  .
The problem asks about the conditional probability P(getting less than 4 given that the result is an odd number).
So, it is P(getting less than 4 | the result is an odd number), and by the definition of conditional probability, it is the ratio
P = P(getting less than 4 AND odd number) / P(the result is an odd number). (1)
The numerator is
.
The problem asks about the conditional probability P(getting less than 4 given that the result is an odd number).
So, it is P(getting less than 4 | the result is an odd number), and by the definition of conditional probability, it is the ratio
P = P(getting less than 4 AND odd number) / P(the result is an odd number). (1)
The numerator is 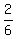 =
=  , because there are only 2 positive odd integers less than 4 (they are 1 and 3)
of 6 possible outputs.
The denominator is
, because there are only 2 positive odd integers less than 4 (they are 1 and 3)
of 6 possible outputs.
The denominator is  , because there are 3 positive odd integer between 1 and 6 inclusive (they are 1, 3 and 5).
Thus the probability under the problem's question is P =
, because there are 3 positive odd integer between 1 and 6 inclusive (they are 1, 3 and 5).
Thus the probability under the problem's question is P = 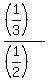 =
=  . ANSWER
. ANSWER
So, the first solution is completed.
The second solution uses the "REDUCED" space of events.
The reduced space of events consists of 3 events getting odd integers between 1 and 6: these events are "1", "3" and "5".
Of them, favorable are only two, "1" and "3".
Therefore, the sough probability is P = 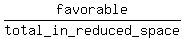 =
=  , giving the same answer.
, giving the same answer.
Thus the second solution is completed, too.
At this point, I stop my teaching.