Question 1182457: Determine whether each ordered pair is a solution to the inequality −5x+2y<0
8,−10)
(0,−5)
(−1,−6)
(−4,−2)
(−7,4)
Found 2 solutions by MathLover1, math_tutor2020:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Determine whether each ordered pair is a solution to the inequality 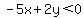
( , , ) )

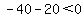
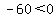 ->true=> ( ->true=> ( , , ) is a solution to the inequality ) is a solution to the inequality
( , , ) )
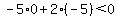

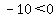 ->true=> ( ->true=> ( , , ) is a solution to the inequality ) is a solution to the inequality
( , , ) )
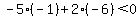
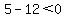
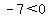 ->true=> ( ->true=> ( , , ) is a solution to the inequality ) is a solution to the inequality
( , , ) )

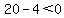
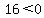 ->false=> ( ->false=> ( , , ) is ) is  a solution to the inequality a solution to the inequality
( , , ) )
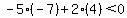
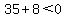
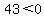 ->false=> ( ->false=> ( , , ) is ) is  a solution to the inequality a solution to the inequality
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Check out this similar problem
https://www.algebra.com/algebra/homework/expressions/expressions.faq.question.1182456.html
Hopefully that's enough to tackle this current problem. If not, then I'll show you how to solve.
Let's draw the graph.
The boundary line is the equation -5x+2y = 0, which is the same as y = (5/2)x. This line goes through (0,0) and (2,5). We make the boundary line a dashed line to tell the reader "points on the boundary are not solutions".
If we plugged in the coordinates of choice A(8,-10), then we get
-5x+2y < 0
-5(8)+2(-10) < 0
-40-20 < 0
-60 < 0
This is a true statement since -60 is smaller than 0. On a number line, -60 is to the left of 0. The last inequality being true indicates the first one is true when (x,y) = (8,-10)
Because -5x+2y < 0 is true for choice A, this means we shade the entire region in which point A is located. This shades below the dashed boundary line as shown below
Graph of -5x+2y < 0

Points A, B, C are in the shaded region. Therefore, they are solution points. In contrast, points D and E are not solutions as they are outside the shaded region.
A non-visual approach is to plug the coordinates of each point into the inequality to see which result in true statements or not. You should find that points A through C result in true statements while D and E lead to false statements.
Here's an example of a false statement
We'll plug in the coordinates for choice D
-5x+2y < 0
-5(-4)+2(-2) < 0
20-4 < 0
16 < 0
we can see this is false because it should be 16 > 0
|
|
|