 The bottom △BCD is isosceles, so we draw the median DE, which is also
the perpendicular bisector of the base, and also the bisector of the vertex
angle D. So it bisects the angle into two 35o angles.
The bottom △BCD is isosceles, so we draw the median DE, which is also
the perpendicular bisector of the base, and also the bisector of the vertex
angle D. So it bisects the angle into two 35o angles.


 Multiply both sides by 15
Multiply both sides by 15

 So the base of △ABC is BC which is twice that amount, so
So the base of △ABC is BC which is twice that amount, so
 Now we need the altitude of △ABC, which is AC
Now we need the altitude of △ABC, which is AC

 Multiply both sides by AC
Multiply both sides by AC


 Area of △ABC =
Area of △ABC = 
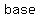

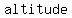 Area of △ABC =
Area of △ABC = 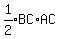 Area of △ABC =
Area of △ABC = 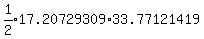 Area of △ABC =
Area of △ABC = 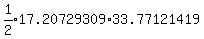 Area of △ABC =
Area of △ABC =  Rounded to two decimal places, 290.56
Edwin
Rounded to two decimal places, 290.56
Edwin