SOLUTION: What is the nth term for the following sequence: 10, 30, 60, 100, 150, 210, ...

Click here to see ALL problems on Sequences-and-series

Question 1182229: What is the nth term for the following sequence:
10, 30, 60, 100, 150, 210, ...
Found 3 solutions by greenestamps, MathLover1, Edwin McCravy:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

If each term is divided by 10, the sequence is

1, 3, 6, 10, 15, 21, ...

You might recognize that sequence as the triangular numbers; or as the sequence in which the n-th term is the sum of the integers 1 through n.

The formula for the n-th triangular number is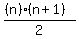

So the n-th term of this sequence is

ANSWER: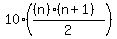

Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!

given: ,,,,,
Sequence : ...................................
First diff. : .........................................
Second diff. : ..................................

We see that the second differences are all equal so we concludet that this is a quadratic sequence.
The quadratic sequence has the form:

To find the value of we just divide second difference ( ) with .

Now we have:

Substitute and into above equation:
if ,

....eq.1

if ,

.....eq.2
from eq.1 and eq.2 we have

go to
....eq.1, substitute

then nth term equation is:

Answer by Edwin McCravy(20054)   (Show Source):
You can put this solution on YOUR website!

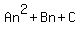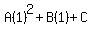
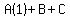
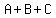
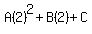
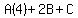
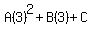
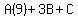
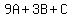10, 30, 60, 100, 150, 210, ... Find the sequence of differences to see if it is an arithmetic sequence 30-10, 60-30, 100-60, 150-100, 210-150, ... Simplifying 20, 30, 40, 50, 60, ... This is an arithmetic sequence, so the nth term is quadratic: Substitute n=1,2,3, a_n = 10, 20 and 30 That gives us the system of equations to solve: The solution is A=5, B=5, C=0 So the nth term 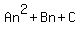becomes or Edwin