Question 1182081: I have tried to understand the answer given to question 870229 but I am struggling with the initial translation of words into algebraic relationships. It doesn’t look correct to me, for example, it looks like the given solution falsely assumes that the motorboat travels 1km in one hour but there is no statement to indicate the time actually taken to travel that 1km.
The question does say the motorboat does travel “one more hour upstream at the same speed” but this doesn’t mean the first km took one hour to traverse. Eg. If the first km took 10hr, it is completely possible to “travel one more hour at the same speed “. Clearly an assumption of 1km/hr is wrong in such a case.
What am I missing here? How can the given solution claim that the first km was traveled in one hour?
I am very grateful if someone can help me understand this as I find the translation of problems in words to algebraic relationships to be my biggest challenge.
The original question is repeated below:
A river flows with uniform velocity v. A person in a motorboat travels 1km upstream, at which time a log is seen floating by. The person continues to travel upstream for one more hour at the same speed and then returns downstream to the starting point, where the same log is seen again. Find the velocity of the river. (Hint: The time of travel of the boat after it meets the log equals the time of travel of the log.)
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52901)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A river flows with uniform velocity v. A person in a motorboat travels 1 km upstream,
at which time a log is seen floating by.
The person continues to travel upstream for one more hour at the same speed
and then returns downstream to the starting point, where the same log is seen again.
Find the velocity of the river.
(Hint: The time of travel of the boat after it meets the log equals the time of travel of the log.)
~~~~~~~~~~~~~~
Let u be the speed of the boat in still water (in km/h).
and let v be the speed of the river ( == the speed of the current ).
(1) First, person travels 1 km upstream.
(2) At that time, he sees the log floating by. Let call this position "the meeting point".
(3) The person continue to travel upsteam for 1 more hour.
During this hour, the person travels (u-v) km upstream.
During this hour, the log travels v kilometers downstream with the current.
(4) Then the person turns back, travels downstream and reaches the starting point at the same time as the log comes to this point.
+----------------------------------------------+
| Let's consider kinematic, starting from |
| the "meeting point" to the ending moment. |
+----------------------------------------------+
During this time, the log travel 1 km with the current speed.
The motorboat travels 1 hour u-v kilometers upstream, and then travels ((u-v)+1)) kilometers DOWNSTREAM with the speed of (u+v) km/h.
So, the log's travel time from the meeting point to the end is  hours;
the motorboat's travel time from the meeting point to the end is hours;
the motorboat's travel time from the meeting point to the end is 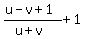 hours.
The two travel times are the same, giving this "time equation" hours.
The two travel times are the same, giving this "time equation"
 = = 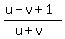 + 1 hours.
OK. The setup is done. Now our task is to solve the equation.
For it, multiply both sides by v*(u+v). You will get
u + v = v*(u-v+1) + v*(u+v)
u + v = vu - v^2 + v + vu + v^2
u = vu + vu
u = 2vu
Now divide both sides by u (which is not a zero, so we can divide safely) and get
1 = 2v
v = + 1 hours.
OK. The setup is done. Now our task is to solve the equation.
For it, multiply both sides by v*(u+v). You will get
u + v = v*(u-v+1) + v*(u+v)
u + v = vu - v^2 + v + vu + v^2
u = vu + vu
u = 2vu
Now divide both sides by u (which is not a zero, so we can divide safely) and get
1 = 2v
v =  .
The problem is just solved ( by a miraculous way (!) ).
ANSWER. The speed of the river (== the speed of the current) is .
The problem is just solved ( by a miraculous way (!) ).
ANSWER. The speed of the river (== the speed of the current) is  km/h. km/h.
Solved, and carefully explained.
/////////////
It is one of the classic, advanced and the most "delicious" Travel & Distance problems.
Do not forget to post your "THANKS" to me for my teaching.
If something is unclear to you in my solution, make a sketch
and mark in this sketch all the mentioned points, times and distances.
The key point in the solution is to get the setup equation, which I called "the time equation".
As soon as you get it, the rest is just a technique.
It is just a technique, but one miraculous moment still takes place (!)
This miraculous moment is the fact that the problem allows us to get a UNIQUE SOLUTION to equation in two unknowns ( ! )
Thanks to the mother-nature and to persons who invented/composed this miraculous problem many years ago ( ! )
\\\\\\\\\\\\\\\\
The post-solution note.
As you understand from my post, I solved this problem INDEPENDENTLY from the solution to this problem
given in the archive MANY YEARS AGO (question 870229; the link
https://www.algebra.com/algebra/homework/word/travel/Travel_Word_Problems.faq.question.870229.html )
Now, couple hours after submitting my post, I looked at the archive' solution to this problem by @mananth.
My DIAGNOSIS after looking at that post is that @mananth INCORRECTLY interprets the problem
and THEREFORE incorrectly solves it.
This so called "tutor" is very well known at this forum as a person who REGULARLY produces wrong solutions.
This problem is DEFINITELY of the much higher level than his (or her).
So, simply ignore his / (her) post, for your safety.
Thank you for paying your attention to this really nice problem (!)
Thanks to you, the wrong solution is neutralized now, and the problem obtains an adequate worthy solution.
I will post my solution in archive to place it under the same question number 870229.
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have tried to understand the answer given to question 870229 but I am struggling with the initial translation of words into algebraic relationships. It doesn’t look correct to me, for example, it looks like the given solution falsely assumes that the motorboat travels 1km in one hour but there is no statement to indicate the time actually taken to travel that 1km.
The question does say the motorboat does travel “one more hour upstream at the same speed” but this doesn’t mean the first km took one hour to traverse. Eg. If the first km took 10hr, it is completely possible to “travel one more hour at the same speed “. Clearly an assumption of 1km/hr is wrong in such a case.
What am I missing here? How can the given solution claim that the first km was traveled in one hour?
I am very grateful if someone can help me understand this as I find the translation of problems in words to algebraic relationships to be my biggest challenge.
The original question is repeated below:
A river flows with uniform velocity v. A person in a motorboat travels 1km upstream, at which time a log is seen floating by. The person continues to travel upstream for one more hour at the same speed and then returns downstream to the starting point, where the same log is seen again. Find the velocity of the river. (Hint: The time of travel of the boat after it meets the log equals the time of travel of the log.)
The response below is for Problem # 870229. Note that you got a response from one of the WORST persons in this forum. That's why you were confused because that person has ABSOLUTELY no idea how to solve simple problems, much less a somewhat complex TRAVEL problem such as this. It's as they say, "You get what you paid for!" Luckily, you didn't pay for the LOUSY/RIDICULOUS answer you received.
Now, getting to the problem at hand, it should be noted that velocity/speed is in 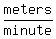 Let speed of boat be S
With the river’s speed being v, the time taken to travel 1,000 m upstream, when log is 1st spotted =
Let speed of boat be S
With the river’s speed being v, the time taken to travel 1,000 m upstream, when log is 1st spotted = 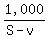 Time taken to travel further upstream: 60 m
Distance traveled upstream, after log was spotted: 60(S - v) = 60S - 60v
Total distance traveled, one-way upstream (also distance downstream, back to starting point) = 1,000 + 60S - 60v
Returning to the starting point, after turning around means that another 1,000 + 60S - 60v was traveled. However, the return distance, being DOWNSTREAM, was at an average speed of S + v
We then get the time taken to travel DOWNSTREAM as:
Time taken to travel further upstream: 60 m
Distance traveled upstream, after log was spotted: 60(S - v) = 60S - 60v
Total distance traveled, one-way upstream (also distance downstream, back to starting point) = 1,000 + 60S - 60v
Returning to the starting point, after turning around means that another 1,000 + 60S - 60v was traveled. However, the return distance, being DOWNSTREAM, was at an average speed of S + v
We then get the time taken to travel DOWNSTREAM as: 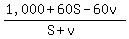 The log was again spotted at the starting point, so, in the time it took the boat to go further upstream - after spotting log the 1st time - turn around and then back to the starting point, the log had traveled 1,000 m, DOWNSTREAM
The SPEED of the log is the speed of the river’s current, or v. Therefore, time taken for the log to travel from the spot itw’s 1st seen, DOWNSTREAM, to the starting point =
The log was again spotted at the starting point, so, in the time it took the boat to go further upstream - after spotting log the 1st time - turn around and then back to the starting point, the log had traveled 1,000 m, DOWNSTREAM
The SPEED of the log is the speed of the river’s current, or v. Therefore, time taken for the log to travel from the spot itw’s 1st seen, DOWNSTREAM, to the starting point = 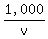 Time it took the log to travel from the 1st time itw’s seen, to the starting point:
Time it took the log to travel from the 1st time itw’s seen, to the starting point: 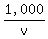 Time taken for the boat to travel upstream, after seeing log: 60 minutes
Time taken by boat to travel downstream, back to starting point, after turning around:
Time taken for the boat to travel upstream, after seeing log: 60 minutes
Time taken by boat to travel downstream, back to starting point, after turning around: 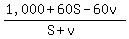 Therefore, we get the following TIME equation:
Therefore, we get the following TIME equation: 
 ------ Reducing fractions by dividing by numerator-GCF, 20 ------ Reducing fractions by dividing by numerator-GCF, 20
 ------- Multiplying by LCD, v(S + v) ------- Multiplying by LCD, v(S + v)
 River’s velocity/speed, or
River’s velocity/speed, or  Note that both problems are the same; however, one uses velocity/speed in
Note that both problems are the same; however, one uses velocity/speed in 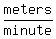 , while the other uses , while the other uses 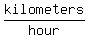 .
My answer: .
My answer: 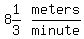 is the same, when converted, as is the same, when converted, as 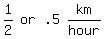 . .
|
|
|