SOLUTION: Prove that the sum of the three altitudes of a triangle is less than the sum of three sides of a triangle.

Let "a", "b" and "c"  be  the lengths of the three sides of the triangle.


Let f, g and h  be  the altitudes of the triangle, drawn to the sides "a", "b" and "c", respectively.


Then we have

    f <= b  and  f <= c;                            (1)

    so  2f <= b+c,  which means  f <= 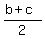.       (2)


Notice that of the two inequalities (1), at least one inequality is the STRICT inequality;
therefore, the final inequality (2) is the STRICT inequality, too,
so we can write instead of (2) strict inequality

        f < 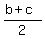.                                  (3)


Similarly to inequality (3), we can prove the following two inequalities

        g < 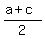,                                  (4)

        h < 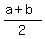.                                  (5)


Now add inequalities  (3), (4) and (5).  You will get

        f + g + h < ,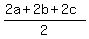

or

        f + g + h < a + b + c.


It is exactly what should be proved.