Question 118175: Our class got assigned a project on polynomials involving writing a research paper and completing a packet of examples, etc. I'm having some trouble on one of the pages in our packet which deals with making "generalizations" about different polynomial functions.
.
It lists the degree of the function along the left side of the page (everything is in a chart format) and then from the degrees listed (which are 0, 1, 2, 3, 4, and 5), we are to write the general form [ f(x)= ], possible number of zeros, possible number of local extrema, and the last box reads "Is there an absolute extrema? (yes, no)".
.
So far, for the general forms of the functions, I've written f(x)=n (n=real number, such as 0, 1, 2...) for the 0 degree, f(x)=x+n for the 1 degree, f(x)=x^2+x+n for the 2 degree, etc. up to f(x)=x^5+x^4+x^3+x^2+x+n for the 5 degree. I think that the general forms I've written are correct, but I wasn't quite sure if the 0 degree would be f(x)="n".
.
For the possible number of zeros I wrote 0 or infinitely many (if f(x)=0) for the 0 degree, 1 for the 1 degree, less than or equal to 2 for the 2 degree, less than or equal to 3 for the 3 degree, up to less than or equal to 5 for the 5 degree. In this column I wasn't sure about the 0 and 1 degree answers...
.
For the possible number of local extrema I wrote 0 for the 0 degree, 0 for the 1 degree, 1 for the 2 degree, less than or equal to 2 for the 3 degree, less than or equal to 3 for the 4 degree, and less than or equal to 4 for the 5 degree. Once again, I wasn't sure about the 0 and 1 degrees...
.
Then comes the absolute extrema column! This column REALLY confuses me!!! I've been looking online for answers as to what exactly an absolute extrema is (because our teacher hasn't taught us this unit yet and the information is not in our books either) and everything has been really hard for me to understand. From what I've gathered it seems like an absolute extrema is just a local extrema but it's the highest or lowest one (if that makes sense to you...). But this then leads me to the problem of answering the question listed in the column, "Is there an absolute extrema? (yes, no)". Would all of the answers be yes, or would infinity not be an acceptable answer? Do you think that the answer could only be yes if it was a definable, or writable (is that even a word?), answer? This column is really troubling me, as you can probably tell...
.
I would REALLY appreciate any help anyone could give me on the "Is there an absolute extrema? (yes, no)" column, as well as any assurance on my answers in the other columns, as well. I'm really sorry for having anyone going to the trouble of helping me with this. For some reason our teacher assigned us this whole project without teaching the information to us; maybe she assumed we just already knew the information? And we didn't have any opportunites of consulting her about the assignment either, as it was assigned to us just before we got out for Winter Break and is due as soon as we get back... But regardless, we cannot change the past, and I would just REALLY appreciate whatever help anyone can contribute! Thank-you so much for even taking the time to read this! I hope you can help!
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The standard form of a polynomial is
 + . . . + . . . 
The 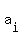 are real numbers and are called coefficients. The term are real numbers and are called coefficients. The term  is assumed to be non-zero and is called the is assumed to be non-zero and is called the  term. The term. The 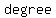 of the polynomial is the of the polynomial is the 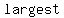 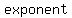 of of  which appears in the polynomial; it is also the subscript on the leading term. which appears in the polynomial; it is also the subscript on the leading term.
A polynomial with 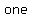 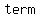 is called a is called a . .
A 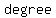 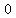 polynomial is a polynomial is a 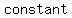 . .
A 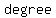 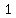 polynomial is a polynomial is a 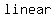  , ,
a 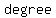  polynomial is a polynomial is a  function, function,
a 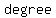  polynomial a polynomial a  , ,
a 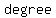  a a 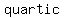 , and so on. , and so on.
the general forms you have written are correct
the possible number of zeros you wrote 0 or infinitely many…
If a polynomial  has a has a   , then , then  can be can be 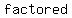 as as

for some polynomial  . This precludes an . This precludes an  degree polynomial from having more than degree polynomial from having more than  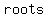 . .
For example, if a quadratic polynomial had  roots, we would have roots, we would have
 . .
But this is  possible since the right-hand side contains at least an possible since the right-hand side contains at least an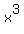 term. term.
Constant function is a function  this function an input, ignores it, and this function an input, ignores it, and 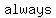 gives the gives the 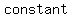  as an output. It is a polynomial of the as an output. It is a polynomial of the  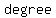 . .
Zero function is  , and it is a special case of the constant function . It is a polynomial of the , and it is a special case of the constant function . It is a polynomial of the  . .
 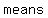 nothing, nothing, 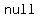 , void or an , void or an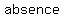 of of . .
In 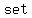 theory, the number zero is the size of the theory, the number zero is the size of the 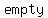 set. A set. A   is a function with is a function with  as its as its  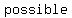 output value. A particular output value. A particular   is a is a  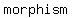 . A . A   is the identity in the additive group of functions. is the identity in the additive group of functions.
 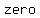 of a function is a preimage of zero, also called the of a function is a preimage of zero, also called the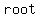 of a function. of a function.
Domain
The 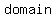 of a function is the set of all points over which it is defined; or simply, it represents the of a function is the set of all points over which it is defined; or simply, it represents the 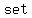 of of 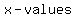 which the function which the function   as input. as input.
The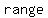 of a function is the of a function is the 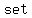 of all of all 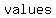 which it attains (i.e. the y-values). which it attains (i.e. the y-values).
 has a has a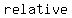 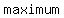 at at  if there is some interval ( if there is some interval ( , ,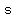 ) (even a very small one) containing ) (even a very small one) containing  for which for which  for all for all 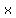 between between  and and  for which for which  is defined. is defined.
 has a has a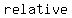 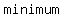 at at  if there is some interval ( if there is some interval ( , ,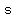 ) (even a very small one) containing ) (even a very small one) containing  for which for which  for all for all 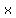 between between  and and  for which for which  is defined. is defined.
By a   , we mean either a , we mean either a  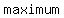 or a or a  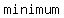 . .
Absolute Maxima and Minima
Relative extrema may sometimes also be absolute extrema, as the following definition shows.
 has an has an  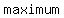 at at  if if  for for 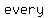  in the in the 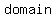 of of  . .
 has an has an  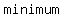 at at  if if  for for 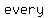  in the in the 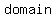 of of  . .
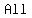  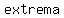 are automatically are automatically  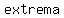 , according to our convention. , according to our convention.
|
|
|