Question 1181566: Find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution. Then determine if the events are unusual. If convenient, use the appropriate probability table or technology to find the probabilities.
Assume the probability that you will make a sale on any given telephone call is 0.13. Find the probability that you (a) make your first sale on the fifth call, (b) make your sale on the first, second, or third call, and (c) do not make a sale on the first three calls.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52814)   (Show Source):
You can put this solution on YOUR website! .
Find the indicated probabilities using the geometric distribution, the Poisson distribution, or the binomial distribution.
Then determine if the events are unusual. If convenient, use the appropriate probability table or technology
to find the probabilities.
Assume the probability that you will make a sale on any given telephone call is 0.13. Find the probability that you
(a) make your first sale on the fifth call,
(b) make your sale on the first, second, or third call, and
(c) do not make a sale on the first three calls.
~~~~~~~~~~~~~~~~~~~
(a) "First sale is on the fifth calls" MEANS that 4 first trials were unsuccessful, and the 5th trial was successful
P = 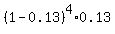 = 0.0745 = 7.45% (rounded). ANSWER
(b) "make your sale on the first, second, or third call" means that SOME one of the 3 trials was successful,
while two other trials were unsuccessful. In this interpretation, it is classic BINOMIAL distribution problem
P = 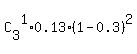 =  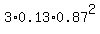= 0.2952 = 29.52% (rounded). ANSWER (see my comment at the end of my post)
(c) "do not make a sale on the first three calls" MEANS that these tree 3 trials were all unsuccessful
P = (1-0.13)*(1-0.13)*(1-0.13) = 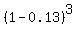 =  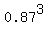= 0.6585 = 65.85% (rounded). ANSWER
@greenestamps was right noticing my error in part (b) (I misread the problem) - - - thanks for it.
After getting his note, I changed this part and fixed this fault.
Now you see the corrected version there.
/\/\/\/\/\/\/\/
The problem is just solved - - - all the questions are answered and explained.
------------
Happy learning (!)
Do not forget to post your "THANKS" to me for my teaching.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
The responses from the other tutor are correct for parts (a) and (c).
For part (b), the statement of the problem is that we are to find the probability that we "make our sale on the first, second, or third call".
That statement is logically nonsense. The "or" indicates we are talking about a particular call; but the "first, second, or third..." indicates we are talking about one of three calls.
To make sense, part (b) should ask for the probability that the FIRST sale is made on the first, second, or third call.
But since that is not what the problem (as you show it) asks for; we can't know what probability they are really asking for. But it definitely does not mean what the other tutor interpreted it as -- making sales on ALL THREE of the first three calls.
|
|
|
