SOLUTION: How many "words" can be made from letters of the word CATERING using different permutations, according to the following rules. 1. Two vowels and two consonants must be used with

First notice that there are 8 letters in all; of them, 3 are vowels and 5 are consonants.


(1)  We can select 2 vowels     from 3 vowels     by   =  =  3 different ways.
 
     We can select 2 consonants from 5 consonants by 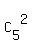  =  = 10 different ways.

     We can combine these sets in 2*10 = 20 different ways.

     Finally, we can order (arrange) each of these sets in 4! = 4*3*2*1 = 24 different ways.


     Applying the fundamental counting principle, we get the total number of possible combinations as 

                  3*10*24 = 30*24 = 720.   ANSWER




(2)  We can select 3 vowels     from 3 vowels     by 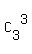  = 1 different ways.
 
     We can select 1 consonants from 5 consonants by 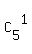  = 5 different ways.

     We can combine these sets in 1*5 = 5 different ways.

     Finally, we can order (arrange) each of these sets in 4! = 4*3*2*1 = 24 different ways.


     Applying the fundamental counting principle, we get the total number of possible combinations as 

                  1*5*24 = 5*24 = 120.   ANSWER




(3)  In this case, we combine 2 vowels and 4 consonants  OR  3 vowels and 3 consonants - and we have no other opportunities.


     Applying the same logic, we have the formula

        total number of arrangements = 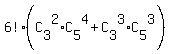 = 720*(3*5 + 1*10) = 720*25 = 18000.    ANSWER