SOLUTION: Given (-1,1), (9,1) and (9,4) (a) find the length of each side of the right triangle, and (b) show that these lengths satisfy the Pythagorean Theorem.

Algebra ->  Triangles -> SOLUTION: Given (-1,1), (9,1) and (9,4) (a) find the length of each side of the right triangle, and (b) show that these lengths satisfy the Pythagorean Theorem.      Log On


   

Question 1181491: Given (-1,1), (9,1) and (9,4)

(a) find the length of each side of
the right triangle, and (b) show that these
lengths satisfy the Pythagorean Theorem.
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Given
(-1,1),
(9,1)
(9,4)
(a) find the length of each side of the right triangle
the length of the side with endpoints (-1,1) and (9,1) is the distance between these two points
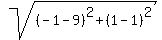
sqrt%28%28-1-9%29%5E2%2B%281-1%29%5E2%29
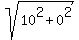
sqrt%2810%5E2%2B0%5E2%29
+10
the length of the side with endpoints (-1,1) and (9,4) is the distance between these two points
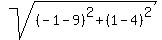
sqrt%28%28-1-9%29%5E2%2B%281-4%29%5E2%29
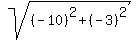
sqrt%28%28-10%29%5E2%2B%28-3%29%5E2%29
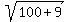
sqrt%28100%2B9%29
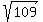
sqrt%28109%29
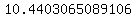
10.4403065089106
the length of the side with endpoints (9,1) and (9,4) is the distance between these two points
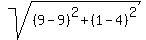
sqrt%28%289-9%29%5E2%2B%281-4%29%5E2%29
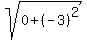
sqrt%280%2B%28-3%29%5E2%29
sqrt%289%29
3

(b) show that these lengths satisfy the Pythagorean Theorem

%2810.4403065089106%29%5E2=10%5E2%2B3%5E2
109=100%2B9
109=109
so, these lengths satisfy the Pythagorean Theorem

Answer by MathTherapy(10556) About Me  (Show Source):
You can put this solution on YOUR website!

Given (-1,1), (9,1) and (9,4)

(a) find the length of each side of
the right triangle, and (b) show that these
lengths satisfy the Pythagorean Theorem.
First, let's label these points, as follows: 

You should notice that points A and B have the same y-coordinate, 1. This means that this is a HORIZONTAL line that's parallel to the x-axis.
This also means that the length of AB is the ABSOLUTE difference between its x-coordinates, or in this case, |- 1 - 9|, or 9 - - 1, = 10.

You may also notice that points B and C have the same x-coordinate, 9. This means that this is a VERTICAL line that's parallel to the y-axis. 
This means that the length of BC is the ABSOLUTE difference between its y-coordinates, or in this case, |1 - 4|, or 4 - 1, = 3.

With AB = 10, and BC = 3, if ABC is right-angled, we will have: 

We do need to find the length of AC since the 2 points have no coordinates in common. This is calculated as: 

This proves that the triangle with coordinate points, (- 1, 1), (9, 1) and (9, 4) is right-angled, as it satisfies the Pythagorean Theorem/Formula.