|
Question 1181386: Let b1, b2, b3 be 3 vectors over Z5 with dimensions 3x1.
b1, b2, b3 are linearly independent.
A is a matrix over Z5 with dimensions 3x3.
Assuming that B is a matrix with dimensions 3x3 where it’s columns are b1 b2 b3.
If it’s given that:
1 2 4
3 1 2 = A*B
1 2 4
Find a vector basis for the vector space that is the answers for the equation Ax=0. | x’s dimensions are 3x1.
(The answer may include elements of bi (you can define them however you’d like))
Answer by ikleyn(52866)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let b1, b2, b3 be 3 vectors over Z5 with dimensions 3x1.
b1, b2, b3 are linearly independent.
A is a matrix over Z5 with dimensions 3x3.
Assuming that B is a matrix with dimensions 3x3 where it’s columns are b1 b2 b3.
If it’s given that:
1 2 4
3 1 2 = A*B
1 2 4
Find a vector basis for the vector space that is the answers for the equation Ax=0. | x’s dimensions are 3x1.
(The answer may include elements of bi (you can define them however you’d like))
~~~~~~~~~~~~~~~
If matrix B is comprised of vectors b1, b2 and b3 as the columns, then the columns of the matrix A*B are :
1st column of A*B is the vector Ab1
2nd column of A*B is the vector Ab2, and
3rd column of A*B is the vector Ab3.
Next, notice that
(1) in matrix A*B the third column is twice its second column; it means that Ab3 = 2Ab2;
(2) in matrix A*B the sum of the first column and the third column is the vector 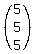 , which over the field Z5 is the same as , which over the field Z5 is the same as  it means that Ab1 + Ab3 is the zero vector in this 3D space
it means that Ab1 + Ab3 is the zero vector in this 3D space 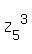 ; in other words, Ab1 + Ab3 = 0.
Notices (1) and (2) combined MEAN that Matrix A has the kernel of the dimension at least 2 over the field ; in other words, Ab1 + Ab3 = 0.
Notices (1) and (2) combined MEAN that Matrix A has the kernel of the dimension at least 2 over the field 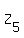 ;
at the same time, the kernel dimension IS NOT 3, as it is seen from the matrix A*B (! it is not a zero matrix ! ) - - - hence,
the dimension of the kernel is EXACTLY 2.
Now, collecting all our observations, we can conclude that the kernel of A has dimension of 2 over the field ;
at the same time, the kernel dimension IS NOT 3, as it is seen from the matrix A*B (! it is not a zero matrix ! ) - - - hence,
the dimension of the kernel is EXACTLY 2.
Now, collecting all our observations, we can conclude that the kernel of A has dimension of 2 over the field 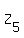 ,
and the basis vectors of the kernel are 2b2- b3 and b1 + b3 ( that are linearly independent !) ,
and the basis vectors of the kernel are 2b2- b3 and b1 + b3 ( that are linearly independent !)
-------------
At this point, the solution is completed.
This problem is intended for students who understand this my explanation and for whom this explanation is enough.
////////////
Please do not forget to post your "THANKS" to me for my teaching (!)
From which University / thinking center / Abstract ALGEBRA textbook / (problems book) is this problem ?
|
|
|
| |