|
Question 1181234: https://media.discordapp.net/attachments/723023718497910816/849263694005403738/unknown.png?width=364&height=117
Found 2 solutions by math_helper, greenestamps:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
You are given r=6cm, h=20cm
The answer can now be determined immediately. How does the volume depend on h? [ That is, is it nonlinear, linear, or not dependent at all ? ]
The LONG way also works:

Let  = Volume of 2nd cone with same radius, and half the volume = Volume of 2nd cone with same radius, and half the volume
 = =  = = 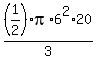
But, also,  = =  where where  is the new height is the new height
Set these last two (Right hand sides) equal
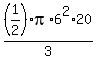 = = 
Note the cancellations:
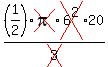 = = 
...leaving:
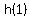 = = 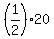 = = 
Understanding the linear relationship between V and h saves a lot of time.
EDIT 6/2:
Sorry, yes, I had the cone flipped upside down so the base was at the bottom.
Of course, I should have realized that makes no sense from a water-filling standpoint!
Answer by greenestamps(13214)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The solution from the other tutor is incorrect.
The picture on the referenced web site shows that the "second" cone does NOT have the same radius of the first; that means the relationship between height and volume is NOT linear.
The "second cone" (the shape of the water in the large cone) is similar to the large cone. The ratio of volumes is 1:2; the ratio of the volumes is the cube of the ratio of the heights (or any other linear measurement).
Let h and H be the heights of the smaller and larger cones, respectively; then

 =0.7937 to 4 decimal places =0.7937 to 4 decimal places
ANSWER: The depth of the water is h=0.7937(20) cm.
Perform the calculation and round as directed.
|
|
|
| |