Question 1181172: five cards are dealt from a well shuffled deck what is the probability that all are face cards
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the number of face cards in the deck is 12 (jack, queen, king, of spades, diamonds, hearts, clubs).
you draw 5 cards from the deck without replacement.
the probability that the first card is a face card is 12/52.
the probability that the second card is a face card is 11/51.
then 10/50, then 9/49, then 8/48.
the probability that all are face cards is therefore:
12/52 * 11/51 * 10/50 * 9/49 * 8/48 = 3.047372795 * 10 ^ -4.
that is equal to .0003047372795 * 100 = .03047372795%.
Answer by greenestamps(13195)  (Show Source):
You can put this solution on YOUR website!
The solution from the other tutor shows one standard method for finding the probability for a problem like this.
There is another basic method you should know, since it is more useful when the problems get more involved.
You are choosing 5 cards from a deck of 52 cards; the number of ways you can do that is "52 choose 5" = C(52,5).
The outcome you want is that all 5 cards are face cards. There are 12 face cards in the deck, so the number of favorable outcomes is 12 choose 5 = C(12,5).
The probability of drawing all face cards is then
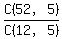 which is about 0.00030474, or 0.03%.
|
|
|
