Question 1181167: Dearest Sir,
Please, I need your help about this problem. Help me solve it and also please show your solution.
Convert the general equation 9𝑥2 + 16𝑦2 − 54𝑥 − 64𝑦 + 1 = 0 to standard form. Sketch and determine the parts of an ellipse.
Solve the value of a, b, and c.
Parts of an Ellipse
1. Center
2. Foci
𝐹1
𝐹2
3. Vertices
𝑉1
𝑉2
4. Co-vertices
𝐵1
𝐵2
5. Endpoints of Latus Rectum
𝐸1
𝐸2
𝐸3
𝐸4
6. Directrices
7. Eccentricity
8. Length of LR
9. Length of Major Axis
10.Length of Minor Axis
Thank a lot and God bless you.
Sincerely yours,
Lorna
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 







 ..........both sides divide by ..........both sides divide by 


=>  , ,  , ,
 => =>
 => =>
 therefore therefore  is semi-major axis and is semi-major axis and  is semi-minor axis is semi-minor axis
 => => => =>
1. Center: ( , , ) )
2. Foci: (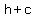 , ,  ), ( ), (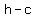 , ,  ) )
F1 ( , ,  ), ( ), (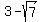 , ,  ) )
F2 (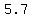 , ,  ), ( ), (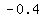 , ,  ) )
3. Vertices: (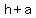 , , ), ( ), (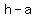 , , ) )
V1 (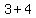 , , ) => ( ) => ( , , ) )
V2 (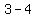 , , ) => ( ) => ( , , ) )
4. Co-vertices ( , ,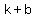 ), ( ), ( , ,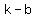 ) )
cV1 ( , ,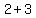 ) =>( ) =>( , , ) )
cV2( , , )=>( )=>( , , ) )
5. Endpoints of Latus Rectum
foci are (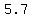 , ,  ), ( ), (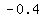 , ,  ) )
endpoints will lie on intersection of the line  and the line and the line  with ellipse with ellipse
 ...substitute ...substitute 
 ...solve for ...solve for 




 or or 
 ...substitute ...substitute 
 ...solve for ...solve for 




 or or 
E1 (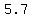 , , 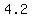 ) )
E2 (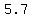 , ,  ) )
E3 (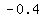 , , 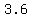 ) )
E4 (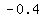 , ,  ) )
6. Directrices:
 =>approximately =>approximately 
 =>approximately =>approximately 
7. Eccentricity: 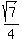 approximately approximately 
8. Length of LR:
9. Length of Major Axis:
10.Length of Minor Axis:

|
|
|