Question 1181166: Dear Sir,
Please help me solve this problem and please show me your solution.
Given by the equation 49𝑥2 + 9𝑦2 = 441, sketch and determine the parts of an ellipse.
Solve for the value a, b, c
Parts of an Ellipse
1. Center
2. Foci
𝐹1
𝐹2
3. Vertices
𝑉1
𝑉2
4. Co-vertices
𝐵1
𝐵2
5. Endpoints of Latus Rectum
𝐸1
𝐸2
𝐸3
𝐸4
6. Directrices
7. Eccentricity
8. Length of LR
9. Length of Major Axis
10.Length of Minor Axis
Thank you very much. More Power.
Sincerely yours,
Lorna
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given by the equation
 ........both sides divide by ........both sides divide by 


=>center is at origin,  , ,
=>
=>
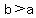 => you have vertical ellipse => you have vertical ellipse





1. Center
2. Foci: ( , , ),( ),( , , ) )
𝐹1 ( , ,  ) )
𝐹2 ( , , 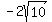 ) )
3. Vertices: ( , , ),( ),( , , ) )
𝑉1 ( , , ) )
𝑉2 ( , , ) )
4. Co-vertices:( , , ),( ),( , , ) )
𝐵1 ( , , ) )
𝐵2 ( , , ) )
5. Endpoints of Latus Rectum
use the coordinate of the focus  , substitute in ellipe equation and solve for , substitute in ellipe equation and solve for 




 ...simplify ...simplify



 or or 
,
𝐸1(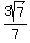 , , ) )
𝐸2(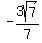 , , ) )
𝐸3(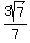 , ,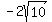 ) )
𝐸4(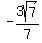 , ,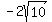 ) )
6. Directrices:  , , 
7. Eccentricity: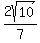
8. Length of LR: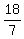
9. Length of Major Axis:
10.Length of Minor Axis:
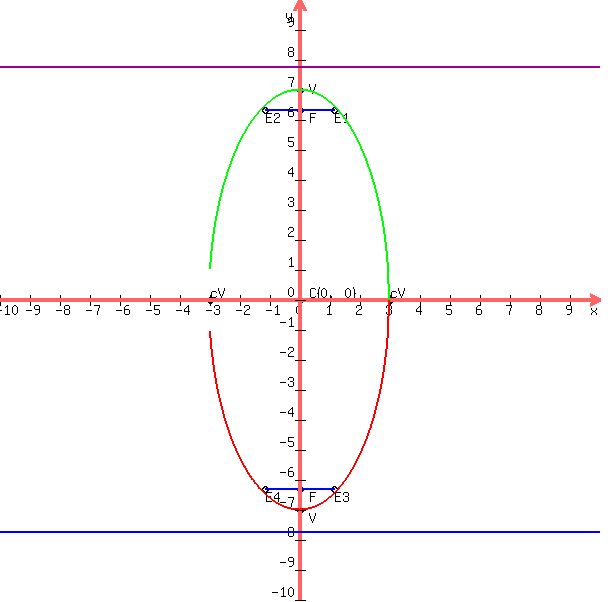
|
|
|