SOLUTION: Given: cos A = 3/5, tan B = 12/5, A is in Quadrant 1 and is in Quadrant 3 Find 1.Sin (A + B) 2.Sin (A - B) 3.Cos (A + B) 4.Cos (A - B) 5.Tan (A - B) 6.Tan ( A+ B)

Algebra ->  Trigonometry-basics -> SOLUTION: Given: cos A = 3/5, tan B = 12/5, A is in Quadrant 1 and is in Quadrant 3 Find 1.Sin (A + B) 2.Sin (A - B) 3.Cos (A + B) 4.Cos (A - B) 5.Tan (A - B) 6.Tan ( A+ B)      Log On


   

Question 1181125: Given: cos A = 3/5, tan B = 12/5, A is in Quadrant 1 and is in Quadrant 3
Find
1.Sin (A + B)
2.Sin (A - B)
3.Cos (A + B)
4.Cos (A - B)
5.Tan (A - B)
6.Tan ( A+ B)
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!
cos A = 3/5, A is in Quadrant 1
sin A =4/5 , cos A = 3/5 , tan A =4/3

tan B = 12/5, quadrant IV
tan B = -12/5, sin B = -12/13 , cos B = 5/13
Sin (A + B) = sin(a)cos(b) + cos(a)sin(b)
= (4/5)(5/13) +(3/5)(-12/13)
= 20/65 - 36/65
-16/65

sin(A − B) = sin A cos B − cos A sin B
=(4/5)(5/13) -(3/5)(-12/13)
56/65
cos(A + B) = cos A cos B − sin A sin B
cos(A − B) = cos A cos B + sin A sin B
sin(A + B) = sin A cos B + cos A sin B
Plug values and continue


Answer by ikleyn(52903) About Me  (Show Source):
You can put this solution on YOUR website!
.

            The numbers and calculations in the post by @mananth are INCORRECT.

            Therefore, for your safety,  IGNORE  his  (or her)  post.

            I came to bring a correct solution. 



cos A = 3%2F5,  A is in Quadrant 1 

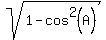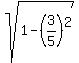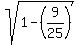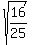sin A = sqrt%281-cos%5E2%28A%29%29 = sqrt%281-%283%2F5%29%5E2%29 = sqrt%281-%289%2F25%29%29 = sqrt%2816%2F25%29%29 = 4%2F5, 

cos A = 3%2F5, tan A = 4%2F3


tan B = 12%2F5, quadrant III   ( ! not quadrant IV, as @mananth mistakenly wrote ! )

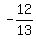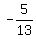tan B = 12%2F5, sin B = -12%2F13, cos B = -5%2F13


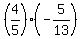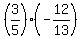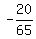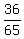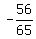sin (A + B) = sin(A)cos(B) + cos(A)sin(B) = %284%2F5%29%28-5%2F13%29 + %283%2F5%29%28-12%2F13%29 = -20%2F65 - 36%2F65 = -56%2F65.


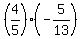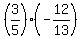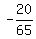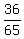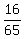sin(A − B) = sin(A)*cos(B) − cos(A)*sin(B) = %284%2F5%29%28-5%2F13%29 - %283%2F5%29%28-12%2F13%29 = -20%2F65 + 36%2F65 = 16%2F65.


cos(A + B) = cos A cos B − sin A sin B 
cos(A − B) = cos A cos B + sin A sin B 
sin(A + B) = sin A cos B + cos A sin B 


Plug values and continue

-------------------

To see many other similar solved problems on calculating trig functions,  look into the lessons
    - Calculating trigonometric functions of angles
    - Advanced problems on calculating trigonometric functions of angles
    - Evaluating trigonometric expressions
in this site.

Also,  you have this free of charge online textbook in ALGEBRA-II in this site
    - ALGEBRA-II - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic  "Trigonometry: Solved problems".


Save the link to this textbook together with its description

Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson

into your archive and use when it is needed.