.
A projectile is fired at an angle of 30 degrees above the horizontal from the top of a cliff 600 ft high.
The initial speed of the projectile is 2000 ft/s. How far will the projectile move horizontally
before it hits the level ground at the base of the cliff?
~~~~~~~~~~~~~~~~~
Vertical component of the initial velocity is half of 2000 ft/s, or 1000 ft/s.
Therefore, the equation for the verical coordinate h(t) is
h(t) = -16t^2 + 1000t + 600
The equation to find the time of the flight is h(t) = 0, or
-16t^2 + 1000t + 600 = 0, or
4t^2 - 250t - 150 = 0.
Its roots are  =
= 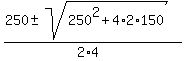 =
= 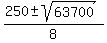 =
=  .
Of these two roots, only positive is interesting for us t =
.
Of these two roots, only positive is interesting for us t = 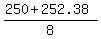 = 62.8 seconds (rounded).
The horizontal component of the speed is
= 62.8 seconds (rounded).
The horizontal component of the speed is  = 1732 ft/s (rouned) and is considered as a constant during the flight.
Moving with the horizontal speed of 1732 ft/s during 62.8 seconds, the projectile will get the ground at the distance of
62.8*1732 = 108769.6 feet from the cliff base. ANSWER
= 1732 ft/s (rouned) and is considered as a constant during the flight.
Moving with the horizontal speed of 1732 ft/s during 62.8 seconds, the projectile will get the ground at the distance of
62.8*1732 = 108769.6 feet from the cliff base. ANSWER
Solved.