You can
put this solution on YOUR website! .
A metallurgist has one alloy containing 22% copper and another containing 53% copper.
How many pounds of each alloy must he use to make 51 pounds of a third alloy containing 30% copper?
(Round to two decimal places if necessary.)
~~~~~~~~~~~~~
Let x be the mass of the 53% copper alloy (in pounds).
Then the mass of the 22% copper alloy is (51-x) pounds.
Now you write equation, saying that the sum of amounts of pure copper in ingredients
is the same as that in the final alloy
0.53x + 0.22*(51-x) = 0.3*51.
From the equation
x = 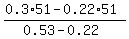 = 13.16 pounds (rounded).
ANSWER. 13.16 pounds of the 53% copper alloy and the rest, (51-13.16) = 37.84 pounds of the 22% copper alloy.
CHECK. I will check the concentration of the final alloy
= 13.16 pounds (rounded).
ANSWER. 13.16 pounds of the 53% copper alloy and the rest, (51-13.16) = 37.84 pounds of the 22% copper alloy.
CHECK. I will check the concentration of the final alloy 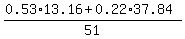 = 0.30, or 30%.
= 0.30, or 30%.
Solved.