Question 1180775: Find the maximum values of the function f(x,y,z)=x^2y^2z^2 subject to the constraint x^2+y^2+z^2=196.
Maximum value is:
My anwer is = 27/7529536 but it's wrong.
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the maximum values of the function f(x,y,z) = x^2y^2z^2 subject to the constraint x^2+y^2+z^2 = 196.
~~~~~~~~~~~~~~~~~
By analogy with the well known AM-GM inequality ("Arithmetic Mean - Geometric Mean inequality") for two variables "a" and "b"
ab <= 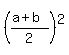 , (1)
there is AM-GM inequality for three variables "a", "b" and "c"
abc <= , (1)
there is AM-GM inequality for three variables "a", "b" and "c"
abc <=  . (2)
Inequalities (1) and (2) are valid for any two and three variables, respectively, that are real non-negative numbers.
In inequalities (1) and (2), equalities are achieved if and only if a = b (for (1)) or a = b = c (for (2)).
Apply inequality (2), taking
a = x^2, b = y^2, c = z^2.
You will get
x^2*y^2*z^2 <= . (2)
Inequalities (1) and (2) are valid for any two and three variables, respectively, that are real non-negative numbers.
In inequalities (1) and (2), equalities are achieved if and only if a = b (for (1)) or a = b = c (for (2)).
Apply inequality (2), taking
a = x^2, b = y^2, c = z^2.
You will get
x^2*y^2*z^2 <=  = =  = = 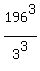 .
Thus the maximum value of x^2*y^2*z^2, under the constraint x^2+y^2+z^2 = 196 is .
Thus the maximum value of x^2*y^2*z^2, under the constraint x^2+y^2+z^2 = 196 is  = = 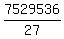 . ANSWER
It is achieved when x^2 = y^2 = z^2 = . ANSWER
It is achieved when x^2 = y^2 = z^2 = 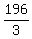 , i.e. x = y = z = +/- , i.e. x = y = z = +/- 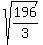 = 8.082904 (rounded).
In all, there are 8 points on the 3D sphere surface x^2 + y^ + z^2 = 196,
where the maximum value of x^2*y^2*z^2 is achieved - one such point in each octant. = 8.082904 (rounded).
In all, there are 8 points on the 3D sphere surface x^2 + y^ + z^2 = 196,
where the maximum value of x^2*y^2*z^2 is achieved - one such point in each octant.
Solved.
///////////////
Do not forget to post your "THANKS" to me for my teaching.
|
|
|