SOLUTION: |7x-3|≤18

The given inequality  | 7x-3 | <= 18  means that  BOTH THESE TWO inequalities are valid


    7x - 3 <= 18    (1)

AND

    -(7x-3) <= 18   (2)



Inequality (1) implies that

    7x <= 18 + 3 = 21,  x <= 3.



Inequality (2) implies that

    -7x <= 18 - 3 = 15,  7x >= -15  (notice that I changed the sign in both sides 
                                     and changed the inequality sign for the opposite one),   

                                    x >= .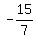


So, the final answer is  the INTERSETION of both partial solution sets 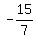  <= x <= 3.