|
Question 118065: Divide. Rationalize the denominator if necessary. Then simplify each radical expression.
1) 18+ square root of 567 OVER 9
2) -9- square root of 108 OVER 3
3) 6- square root of 20 OVER 2
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll do the first two to show you how to do these
#1
Start with the expression
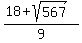
First lets reduce 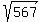
-----------------------------------------------------
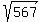 Start with the given expression Start with the given expression
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. This way the perfect square will become a rational number.
So let's list the factors of 567
Factors:
1, 3, 7, 9, 21, 27, 63, 81, 189, 567
Notice how 81 is the largest perfect square, so lets break 567 down into 81*7
 Factor 567 into 81*7 Factor 567 into 81*7
 Break up the square roots using the identity Break up the square roots using the identity 
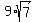 Take the square root of the perfect square 81 to get 9 Take the square root of the perfect square 81 to get 9
So the expression
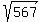
simplifies to
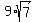
-----------------------------------------------------
 Simplify the square root (using the technique above) Simplify the square root (using the technique above)
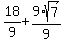 Break up the fraction Break up the fraction
 Divide Divide 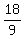 to get to get 
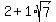 Divide Divide  to get to get 
So the expression
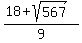
simplifies to
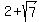
#2
Start with the expression
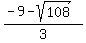
First lets reduce 
-----------------------------------------------------
 Start with the given expression Start with the given expression
The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. This way the perfect square will become a rational number.
So let's list the factors of 108
Factors:
1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108
Notice how 36 is the largest perfect square, so lets break 108 down into 36*3
 Factor 108 into 36*3 Factor 108 into 36*3
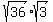 Break up the square roots using the identity Break up the square roots using the identity 
 Take the square root of the perfect square 36 to get 6 Take the square root of the perfect square 36 to get 6
So the expression

simplifies to

-----------------------------------------------------
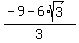 Simplify the square root (using the technique above) Simplify the square root (using the technique above)
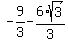 Break up the fraction Break up the fraction
 Divide Divide 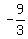 to get to get 
 Divide Divide 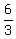 to get to get 
So the expression
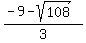
simplifies to

|
|
|
| |