Question 1180531: Find the 3 cube roots of i in polar form.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the 3 cube roots of i in polar form.
~~~~~~~~~~~~~~~~
i = (1,  ) = (1,90°) in polar form (the modulus is 1; the argument is ) = (1,90°) in polar form (the modulus is 1; the argument is  , or 90°).
Use deMoivre formula. The three cubic roots of " i " are
a) (1, , or 90°).
Use deMoivre formula. The three cubic roots of " i " are
a) (1,  ) = (1,30°);
b) (1, ) = (1,30°);
b) (1,  ) = (1, ) = (1, 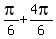 ) = (1, ) = (1, 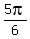 ) = (1,150°);
c) (1, ) = (1,150°);
c) (1, 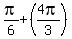 ) = (1, ) = (1, 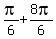 ) = (1, ) = (1, 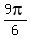 ) = (1,270°). ) = (1,270°).
Solved and explained.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
While correct, neither the notation (r,θ) nor rei*θ is used when teaching complex numbers
in basic trigonometry courses. That's because such notation eliminates the trigonometric functions.
Find the 3 cube roots of i in polar form.
i = 0 + 1i
Graph the vector whose magnitude (modulus) is r=1, whose tail is at (0,0),
and whose tip is at (0,1), and whose argument (angle) is θ=90o.

  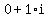  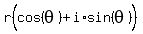 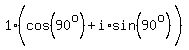 Since the cube root is the 1/3 power:
Since the cube root is the 1/3 power:
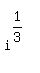  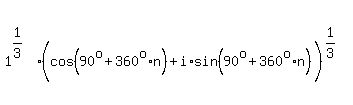 We raise everything to the 1/3 power. In doing so we will use deMoivre's
theorem, where we raise the magnitude (modulus 1) to the 1/3 power (i.e.,
take its cube root 1), and multiply its argument (angle) by 1/3.
We raise everything to the 1/3 power. In doing so we will use deMoivre's
theorem, where we raise the magnitude (modulus 1) to the 1/3 power (i.e.,
take its cube root 1), and multiply its argument (angle) by 1/3.
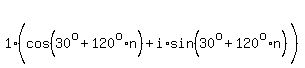 Now, since there are 3 cube roots, we take three consecutive integers for n.
Let n=0
Now, since there are 3 cube roots, we take three consecutive integers for n.
Let n=0
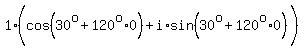  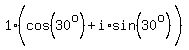 Let n=1
Let n=1
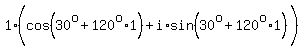  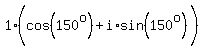 Let n=2
Let n=2
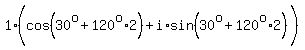  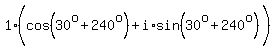  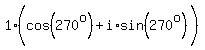 .
Edwin .
Edwin
|
|
|