Question 1180442: You are tasked with assisting a young couple in purchasing a home. The couple wants to buy a house valued at R1 000 000. They intend to put down a deposit of R2 000 000 and repay the remainder over a period of 20 years. If they make payments at the end of each month and interest rate is 12% pear year compounded monthly, calculate their required monthly payments?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this doesn't make sense.
the house is valued at 1 million rands and the deposit is 2 million rands?
i believe the R stands for south african rand, but i could be mistaken.
regardless, if the price of 1 million rands, then the deposit has to be something less than 1 million rands.
2 million rands is greater than 1 million rands.
this is why i say it doesn't make sense.
regqrdless, i can give you the formula to use, or an online calculator to use, for you to determine what is owed at the end of each month.
i will use the price of the house you gave me and include a down payment of 20% of the price of the house, which is standard in the united states.
consequently, the price of the house is 1,000,000 and the down payment is 200,000.
you can substitue whatever numbers you think are more accurate.
here we go, using an online calculator.
the price of the house is 1,000,000
the down payment is 200,000
the amount to be amortized is 800,000.
inputs to the calculator are:
pv = present value = -800000
fv = future value = 0
np = number of time periods = 20 year * 12 months per year = 240 months
ir = interest rate % per time period = 12% / 12 = 1% per month
payment is at the end of each month.
the results from the calculator are that pmt = monthly payment = $8,808.69
the formula to use is:
ANNUITY FOR A PRESENT AMOUNT WITH END OF TIME PERIOD PAYMENTS
a = (p*r)/(1-(1/(1+r)^n))
a is the annuity.
p is the present amount.
r is the interest rate per time period.
n is the number of time periods.
in this formula, ...
p = present amount = 800,000 (without the comma).
r is the interest rate per month = .01 (rate is used, not percent).
the number of time periods = 240 months.
the formula becomes:
a = (800000*.01)/((1-(1/(1+.01)^240)) = 8808.689069.
the formula and the calculator agree.
if you try to do this by formula, make sure you get the parentheses right.
otherwise the answer will not come out correctly.
using the calculator is much easier.
the formula is there just in case you are reuired to do this by formula.
either way, if the cost of the house is 1 million and the down payment is 200 thousand, then the payment at the end of each month is 8808.69 rounded to the nearest penny.
here are the result using the calculator.
inputs:
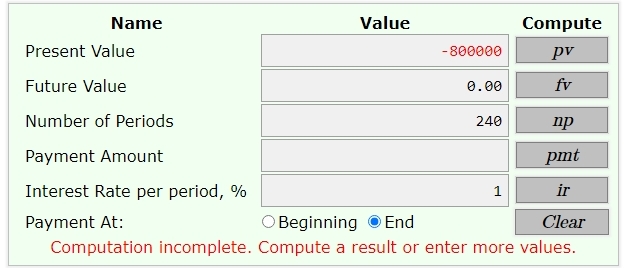
outputs:
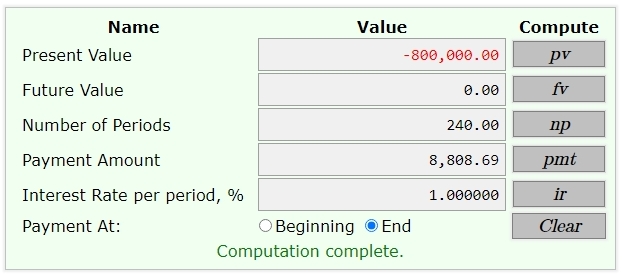
the calculator can be found at https://arachnoid.com/finance/index.html
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As the problem is worded, printed, posted and presented, it is really UNCLEAR what happens and what is
the meaning of this assignment.
If you want to get help and to get real solution to real problem, then please re-post CORRECTLY.
But if you do not understand the subject, at all, and if you do not understand the meaning of words which you use,
then do not re-post.
|
|
|