Question 1180422: Find the maximum area that can be formed by a series of small pens next to a river with separate enclosures as shown. The total length of fencing is 40m.
https://docs.google.com/document/d/1Cl3HrcoR6jibNzxfDTIilS3imSplLY8nQUU0OpU9vLA/edit?usp=sharing
Found 3 solutions by MathLover1, ikleyn, greenestamps:
Answer by MathLover1(20850)   (Show Source):
Answer by ikleyn(52915)  (Show Source):
You can put this solution on YOUR website! .
Find the maximum area that can be formed by a series of small pens next to a river
with separate enclosures as shown. The total length of fencing is 40m.
https://docs.google.com/document/d/1Cl3HrcoR6jibNzxfDTIilS3imSplLY8nQUU0OpU9vLA/edit?usp=sharing
~~~~~~~~~~~~~~
The post by @MathLover1 is irrelevant and incorrect approach.
I came to bring a correct solution.
We have one wall of the length x and 5 (five) walls of the length y
x + 5y = 40 meters. (1)
We want to find maximum area xy under this restriction (1).
From (1), x = 40-5y, so the area is
xy = (40-5y)*y = 40y - 5y^2.
It is a quadratic function of y.
The leading coefficient -5 is negative, so the plot of the function as function of y
is a downward parabola.
The roots of the parabola
40y - 5y^2 = 5y(8-y)
are y = 0 and y = 8; so, the maximum of the parabola is at 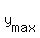 =  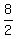= 4
exactly half way between the roots.
Thus the optimal dimensions, giving maximum area are y = 4 m and x = 40-5y = 40-5*4 = 20 m.
The maximum area is 4*20 = 80 square meters.
Solved, answered and explained.
----------------
To see other similar and different solved problems, look into the lessons
- A rectangle with a given perimeter which has the maximal area is a square
- A farmer planning to fence a rectangular garden to enclose the maximal area
- A farmer planning to fence a rectangular area along the river to enclose the maximal area
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13216)  (Show Source):
You can put this solution on YOUR website!
The formal solution from tutor @ikleyn is fine. It is a good example of problem solving using formal algebra; you should understand it.
The solution method shown by the other tutor is NOT irrelevant, as tutor @ikleyn says. It is a fast path to the solution -- IF you use it correctly, which the other tutor did not.
It is relatively easy to prove that in any problem like this, the maximum area is obtained when -- as the other tutor says -- the total amount of fencing is equally divided between the lengths and widths.
So the initial starting point of the other tutor's response was fine; she just didn't use the right numbers.
So while the formal algebraic solution is fine if a formal solution is required, the problem can be solved easily and quickly if an informal solution is allowable.
The total length of fencing is 40m, so we want to use 20m for the length(s) and 20m for the width(s).
In this problem, there is one length of fencing and 5 widths of fencing, so the maximum area is when the length is 20/1=20m and the width is 20/5=4m.
ANSWER: The maximum area is 20m*4m = 80 square meters
|
|
|
