Question 1180354: For two events A and B, P(A) = 0.3 and P(B)=0.2. (a) If A and B are independent, then P(A|B) =
P(A∩B) =
P(A∪B) =
(b) If A and B are dependent and P(A|B) = 0.25,
then P(B|A) =
P(A∩B) =
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! For two events A and B, P(A) = 0.3 and P(B)=0.2. (a) If A and B are independent, then P(A|B) =
P(A∩B) =
P(A∪B) =
(b) If A and B are dependent and P(A|B) = 0.25,
then P(B|A) =
P(A∩B) =
~~~~~~~~~~~~~~~~~~~
I will solve part a), ONLY.
I will answer in other, more natural order.
First, P(A ∩ B) = P(A)*P(B) = 0.3*0.2 = 0.06 (since A and B are independent).
Second, P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.3 + 0.2 - 0.06 = 0.44.
Third, P(A | B) =  = = 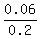 = 0.3. = 0.3.
Solved.
////////////////
One and ONLY ONE problem/question per post.
It is the RULE, the POLICY and the REQUIREMENT of this forum.
It is written in this page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
///////////
Edwin expressed "a favor" in my address - - - so, I will express my favor in his address, mutually.
Ignore his solution: it is INCORRECT:
It is incorrect, because it is based on your incorrect formulation of the part b).
The event A and B must be INDEPENDENT - - - while your formulation
calls them "DEPENDENT" - - - clearly, directly, explicitly and incorrectly.
And Edwin NEITHER disproved NOR corrected it . . .
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Pay no attention to her gripes.
For two events A and B, P(A) = 0.3 and P(B)=0.2. (a) If A and B are independent, then
P(A|B) = P(A∩B) =
P(A∪B) =
Venn diagrams make things easier to understand than formulas alone.
Draw a Venn diagram with sets A and B, with r,s,t,u representing the
probabilities of the four regions:
 P(A) = 0.3 = r+s
P(B) = 0.2 = s+t
Since they are independent,
P(A∩B) = s = P(A)P(B) = (0.3)(0.2) = 0.06 <--ANSWER to P(A∩B)
So since
s = 0.06 and
r+s = 0.3, substitution gives
r+0.06 = 0.3
r = 0.3-0.06
r = 0.24
And since
s = 0.06 and
s+t = 0.2
0.06+t = 0.2
t = 0.14
P(A∪B) = r+s+t = 0.24+0.06+0.14 = 0.44 <--ANSWER to P(A∪B)
P(A) = 0.3 = r+s
P(B) = 0.2 = s+t
Since they are independent,
P(A∩B) = s = P(A)P(B) = (0.3)(0.2) = 0.06 <--ANSWER to P(A∩B)
So since
s = 0.06 and
r+s = 0.3, substitution gives
r+0.06 = 0.3
r = 0.3-0.06
r = 0.24
And since
s = 0.06 and
s+t = 0.2
0.06+t = 0.2
t = 0.14
P(A∪B) = r+s+t = 0.24+0.06+0.14 = 0.44 <--ANSWER to P(A∪B)
 Note: We weren't asked for P(A'∩B') = u, but we could have
found it because r+s+t+u = 1, so
0.24+0.06+0.14+u = 1
0.44+u = 1
u = 0.56
------------------------------------
(b) If A and B are dependent and P(A|B) = 0.25,
then P(B|A) =
P(A∩B) =
Note: We weren't asked for P(A'∩B') = u, but we could have
found it because r+s+t+u = 1, so
0.24+0.06+0.14+u = 1
0.44+u = 1
u = 0.56
------------------------------------
(b) If A and B are dependent and P(A|B) = 0.25,
then P(B|A) =
P(A∩B) =
 P(A|B) = P(A∩B)/P(B) = s/0.2 = 0.25
s = 0.25(0.2)
s = 0.05
P(B|A) = P(B∩A)/P(A) = P(A∩B)/P(A) = s/0.2 = 0.05/0.3 = 5/30 = 1/6
(We could have just divided 0.05 by 0.3 and gotten 0.1666666...,
but repeating decimals are a hassle, so I multiplied top and bottom
by 100 and got the fraction 5/30 which reduced to 1/6.
We aren't asked to, but we could finish out the Venn diagram for (b) if we
like:
P(A|B) = P(A∩B)/P(B) = s/0.2 = 0.25
s = 0.25(0.2)
s = 0.05
P(B|A) = P(B∩A)/P(A) = P(A∩B)/P(A) = s/0.2 = 0.05/0.3 = 5/30 = 1/6
(We could have just divided 0.05 by 0.3 and gotten 0.1666666...,
but repeating decimals are a hassle, so I multiplied top and bottom
by 100 and got the fraction 5/30 which reduced to 1/6.
We aren't asked to, but we could finish out the Venn diagram for (b) if we
like:
 Edwin
Edwin
|
|
|