SOLUTION: Solving for Two Variables using Elimination 4x - 3y = -14 and -x + 3y = -11

Algebra ->  Expressions-with-variables -> SOLUTION: Solving for Two Variables using Elimination 4x - 3y = -14 and -x + 3y = -11      Log On


   

Question 1180313: Solving for Two Variables using Elimination
4x - 3y = -14 and -x + 3y = -11
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Solved by pluggable solver: Solving a System of Linear Equations by Elimination/Addition


Lets start with the given system of linear equations

4%2Ax-3%2Ay=-14
-1%2Ax%2B3%2Ay=-11

In order to solve for one variable, we must eliminate the other variable. So if we wanted to solve for y, we would have to eliminate x (or vice versa).

So lets eliminate x. In order to do that, we need to have both x coefficients that are equal but have opposite signs (for instance 2 and -2 are equal but have opposite signs). This way they will add to zero.

So to make the x coefficients equal but opposite, we need to multiply both x coefficients by some number to get them to an equal number. So if we wanted to get 4 and -1 to some equal number, we could try to get them to the LCM.

Since the LCM of 4 and -1 is -4, we need to multiply both sides of the top equation by -1 and multiply both sides of the bottom equation by -4 like this:

-1%2A%284%2Ax-3%2Ay%29=%28-14%29%2A-1 Multiply the top equation (both sides) by -1
-4%2A%28-1%2Ax%2B3%2Ay%29=%28-11%29%2A-4 Multiply the bottom equation (both sides) by -4


So after multiplying we get this:
-4%2Ax%2B3%2Ay=14
4%2Ax-12%2Ay=44

Notice how -4 and 4 add to zero (ie -4%2B4=0)


Now add the equations together. In order to add 2 equations, group like terms and combine them
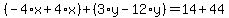
%28-4%2Ax%2B4%2Ax%29%2B%283%2Ay-12%2Ay%29=14%2B44

%28-4%2B4%29%2Ax%2B%283-12%29y=14%2B44

cross%28-4%2B4%29%2Ax%2B%283-12%29%2Ay=14%2B44 Notice the x coefficients add to zero and cancel out. This means we've eliminated x altogether.



So after adding and canceling out the x terms we're left with:

-9%2Ay=58

y=58%2F-9 Divide both sides by -9 to solve for y



y=-58%2F9 Reduce


Now plug this answer into the top equation 4%2Ax-3%2Ay=-14 to solve for x

4%2Ax-3%28-58%2F9%29=-14 Plug in y=-58%2F9


4%2Ax%2B174%2F9=-14 Multiply



4%2Ax%2B58%2F3=-14 Reduce



4%2Ax=-14-58%2F3 Subtract 58%2F3 from both sides

4%2Ax=-42%2F3-58%2F3 Make -14 into a fraction with a denominator of 3

4%2Ax=-100%2F3 Combine the terms on the right side

cross%28%281%2F4%29%284%29%29%2Ax=%28-100%2F3%29%281%2F4%29 Multiply both sides by 1%2F4. This will cancel out 4 on the left side.


x=-25%2F3 Multiply the terms on the right side


So our answer is

x=-25%2F3, y=-58%2F9

which also looks like

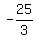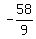(-25%2F3, -58%2F9)

Notice if we graph the equations (if you need help with graphing, check out this solver)

4%2Ax-3%2Ay=-14
-1%2Ax%2B3%2Ay=-11

we get



graph of 4%2Ax-3%2Ay=-14 (red) -1%2Ax%2B3%2Ay=-11 (green) (hint: you may have to solve for y to graph these) and the intersection of the lines (blue circle).


and we can see that the two equations intersect at (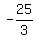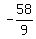-25%2F3,-58%2F9). This verifies our answer.

Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


20-30 lines to solve this pair of equations using elimination is absurd. Adding the two given equations eliminates one of the variables....

4x-3y=-14
-x+3y=-11
3x=-25
x=-25/3

25/3+3y=-11=-33/3
3y=-58/3
y=-58/9

ANSWER: (-25/3,-58/9)