Question 1180262: Show all work. Be sure to answer both part A and B to the following questions.
Part A, Which of the following is a polynomial equation?
a.6x^2 + x + 2 = (6x-2)(x+4)
b.(5x-1)^2 = 25x^2 + 1
c.9(4a^2 - 4ab + b^2) = (6a - 3b)^2
d.(7x + 2)(x - y) = 7x(x - y) - 2y
Part B, Which expression is not equivalent to 16x^4 - y^4?
a.(2x-y)(2x+y)(4x^2 + y^2)
b.(2x)^4 - (y)^4
c.4x^2(4x^2 - y^2) + y^2(4x^2 - y^2)
d.(2x-y)(8x^3 + y^3)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! recall:
A polynomial function is a function that involves only 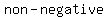 integer integer 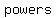 or only or only 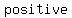 integer integer 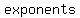 of a variable in an equation like the quadratic equation, cubic equation, etc. For example, of a variable in an equation like the quadratic equation, cubic equation, etc. For example,  is a polynomial. As a general rule of thumb if an algebraic expression has a radical in it then it isn't a polynomial. is a polynomial. As a general rule of thumb if an algebraic expression has a radical in it then it isn't a polynomial.
A zero polynomial is the one where all the coefficients are equal to  . So, the degree of the zero polynomial is either . So, the degree of the zero polynomial is either  , or it is set equal to , or it is set equal to  . .
A polynomial function is made up of terms called monomials.
A monomial is an expression that contains only one term. In other words, a monomial is a polynomial with a single term. Generally, monomials include numbers, variables, or a number and a variable multiplied together, two or more variables multiplied together. A monomial is an expression that does not contain any arithmetic operators.
Part A
a.
 .....expand .....expand
 ..........simplify ..........simplify



 => polynomial => polynomial
b.
 ....expand ....expand
 ..........simplify ..........simplify




 => is polynomial =>classification: a degree => is polynomial =>classification: a degree  polynomial with polynomial with  term and term and  variable variable
c.
 ....expand ....expand
 ........simplify ........simplify
 => is polynomial =>classification: is a degree => is polynomial =>classification: is a degree  polynomial with polynomial with  term and term and  variable variable
d.
 ....expand ....expand
 ........simplify ........simplify


 => is a degree => is a degree  polynomial with polynomial with  term and term and  variable variable
Part B
Which expression is not equivalent to 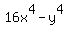 ? ?
a.
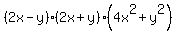 ...expand ...expand
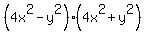
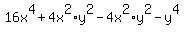
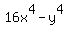 ->expression ->expression  equivalent to equivalent to 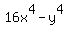
b.
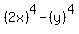
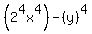
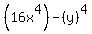 ->expression ->expression  equivalent to equivalent to 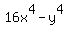
c.
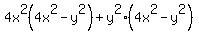
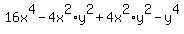
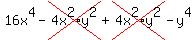
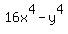 ->expression ->expression 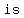 equivalent to equivalent to 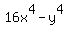
d.
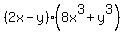
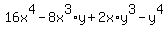 ->expression ->expression   equivalent to equivalent to 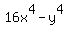
|
|
|