Question 1180259: Identify the equations of ellipses whose major axis lengths are twice their minor axis lengths.
a. 4x^2+25y^2+32x-250y+589=0
b. 2x^2+8y^2-12x+16y-174=0
c. 4x^2+y^2+16x+4y+4=0
d. 3x^2+12y^2+18x-24y-69=0
e. 16x^2+y^2-64x+8y+16=0
f. x^2+9y^2-2x+18y-71=0
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Identify the equations of ellipses whose major axis lengths are twice their minor axis lengths.
recall: recall: The equation of an ellipse is
 -> horizontal major axis, -> horizontal major axis, 
and
 -> vertical major axis, -> vertical major axis, 
The center is ( , , ) and the larger of ) and the larger of  the major axis , the major axis , is minor axis. is minor axis.
a.
 ......competing squares you will get ......competing squares you will get






 ........both sides divide by ........both sides divide by 



 , ,
major axis:
minor axis:
=> major axis length is  twice the length of minor axis twice the length of minor axis
b.




 ....simplify, both sides divide by ....simplify, both sides divide by 


 ........both sides divide by ........both sides divide by 



 , ,
major axis:
minor axis:
=> major axis length 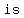 twice the length of minor axis twice the length of minor axis
c.






 ......both sides divide by ......both sides divide by 



 , ,
major axis:
minor axis:
=> major axis length 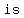 twice the length of minor axis twice the length of minor axis
d.
 ...simplify, both sides divide by ...simplify, both sides divide by 










 , ,
major axis:
minor axis:
=> major axis length 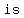 twice the length of minor axis twice the length of minor axis
e.




 ...simplify, both sides divide by ...simplify, both sides divide by 


 .........both sides divide by .........both sides divide by 


 , ,
major axis:
minor axis:
=> major axis length 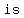  twice the length of minor axis twice the length of minor axis
f.






 .......both sides divide by .......both sides divide by 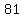



 , ,
major axis:
minor axis:
=> major axis length 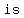  twice the length of minor axis twice the length of minor axis
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's look at the first equation in detail to see if its graph has the major axis twice the minor axis. Then we will look at what it is about the equation in the given form that tells us the ratio of the lengths of the major and minor axes, so we can find the ones we want without doing the complete analysis.
a. 4x^2+25y^2+32x-250y+589=0
Move the constant to the other side and factor out the leading coefficient of the quadratic terms:
4(x^2+8x+___)+25(y^2-10y+___)=-589
Complete the square in both variables, making sure to keep the equation balanced:
4(x^2+8x+16)+25(y^2-10y+25)=-589+64+625=100
(x+4)^2/25+(y-5)^2/4=1
The major axis is sqrt(25)=5; the minor axis is sqrt(4)=2.
No; for this equation, the major axis length is not twice the minor axis length.
----------------------------------------------------------------------
That was a lot of work to find this equation is not one that we are looking for.
Let's look to see if we can identify the ones we want without doing all that work.
The ratio of the lengths of the major and minor axes in this example was sqrt(25)/sqrt(4) = 5/2.
But the "25" and "4" are the coefficients of the x^2 and y^2 terms in the given equation (although in the opposite order, but we don't care about that).
So a necessary and sufficient condition for the ratio of the lengths of the major and minor axes to be 2:1 is that the ratio of the coefficients of the x^2 and y^2 terms in the given equation be 4:1, or 1:4.
Now we can dispense with the rest of the problem easily.
a. 4x^2+25y^2+32x-250y+589=0
NO. 4:25 is not 1:4
b. 2x^2+8y^2-12x+16y-174=0
YES. 2:8 = 1:4
c. 4x^2+y^2+16x+4y+4=0
YES. 4:1
d. 3x^2+12y^2+18x-24y-69=0
YES. 3:12 = 1:4
e. 16x^2+y^2-64x+8y+16=0
NO. 16:1 is not 4:1
f. x^2+9y^2-2x+18y-71=0
NO. 1:9 is not 1:4
|
|
|