Question 1180205: What are the possible number of positive, negative and imaginary zeros of:
f(x)= x^3 - 11x^2 + 8x - 20
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!

Use Decartes' rule of signs...
So, the coefficients are  , , , , , ,
As can be seen, there are 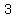 changes. changes.
This means that there are 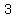 or or  positive real roots. positive real roots.
To find the number of negative real roots, substitute  with with  in the given polynomial: in the given polynomial:
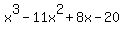 becomes becomes 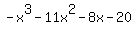
The coefficients are  , , , , , , . .
As can be seen, there are changes. changes.
This means that there are negative real roots. negative real roots.
Answer:
 or or  positive real zeros positive real zeros
 negative real zeros negative real zeros
 or or  imaginary zeros imaginary zeros
|
|
|