Question 1180131: Find the diameter of the circle that can be circumscribed around a triangle that has two 13-inch sides
and one 10-inch side.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13196)   (Show Source):
You can put this solution on YOUR website!
The triangle is isosceles. The altitude to the 10-inch side divides the triangle into two right triangles each with hypotenuse 13 and one leg 10/2=5. By the Pythagorean Theorem, the other leg (the altitude of the triangle) is 12.
The center of the circumscribed circle is on that altitude.
Let x be the radius of the circumscribed circle; the distance from the center of the circle to each vertex of the triangle is then x.
The distance from the center of the circle to the foot of the altitude is then 12-x.
The radius to one of the base vertices, along with portions of the base and altitude of the triangle, form a right triangle with legs 5 and 12-x and hypotenuse x.
Use the Pythagorean Theorem to solve for the radius x; then double that to find the diameter.
Answer by ikleyn(52756)  (Show Source):
You can put this solution on YOUR website! .
Find the diameter of the circle that can be circumscribed around a triangle that has two 13-inch sides
and one 10-inch side.
~~~~~~~~~~~~~~~~
There is a remarcable formula, connecting the area of a triangle, its sides and the radius of the circumscribed circle.
This formula is S =  (1)
where "a", "b", "c" are the triangle' side lengths, S is the triangle formulas and R is the radius of the circumscribed circle.
For the proof of this formula see the lesson
- Proof of the formula for the radius of the circumscribed circle
in this site.
The formula works and is valid for ANY TRIANGLE.
By knowing the side lengths of the given triangle, we can calculate its area using the Hero's formula.
But in the given case, we can calculate the area of the triangle by even simpler way as half the product of the base length (10 inches)
and the height drawn to the base. The height is, obviously, 12 = 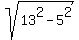 , therefore, the area of the triangle is
S = 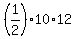 = 60 sq. inches.
Now from the formula (1), the radius of the circumscribed circle is
R =  =  =  .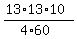
Therefore, the diameter of the circumscribed circle is d = 2R =  . ANSWER
Solved.
|
|
|
