Question 1180070: Based on the equations of the parabolas, identify each parabola whose focus and vertex lie in different quadrants.
a. y=-x^2/8+x/4+23/8
b. y=x^2/32+x/4-13/2
c. x=-y^2/16-y/4+11/4
d. x=y^2/16+y/4-19/4
e. x=-y^2/36-5y/18+299/36
f. y=-x^2/24-5x/12+95/24
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Based on the equations of the parabolas, identify each parabola whose focus and vertex lie in different quadrants.
a.

use vertex form

 ........complete square ........complete square

 ...... ......







=> , ,  , ,  => =>
vertex is at ( , , )=( )=( , , )->Q I )->Q I
focus is at: ( , ,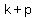 )=( )=( , ,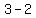 )=( )=( , , )->Q I )->Q I
=>focus and vertex lie in 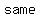 quadrant quadrant
b.


 ....... .......






=> , ,  , ,  => =>
vertex is at ( , , )=( )=( , , )->Q III )->Q III
focus is at: ( , ,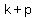 )=( )=( , ,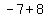 )=( )=( , , )->Q II )->Q II
=>focus and vertex lie in 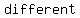 quadrants quadrants
c.

 .... ....






=> , ,  , ,  => =>
vertex is at ( , , )=( )=( , , ) ->Q VI ) ->Q VI
focus is at: ( , , )=( )=(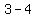 , , )=( )=( , , ) ->Q III ) ->Q III
=>focus and vertex lie in 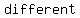 quadrants quadrants
d.








=> , ,  , ,  => =>
vertex is at ( , , )=( )=( , , ) ->Q III ) ->Q III
focus is at: ( , , )=( )=(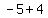 , , )=( )=( , , ) ->Q III ) ->Q III
=>focus and vertex lie in 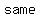 quadrant quadrant
e.

 ......... .........





=> , ,  , ,  => =>
vertex is at ( , , )=( )=( , , ) ->Q IV ) ->Q IV
focus is at: ( , , )=( )=(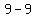 , , )=( )=( , , ) ->between Q III and Q IV ) ->between Q III and Q IV
=>focus and vertex lie in 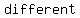 quadrants quadrants
f.







=> , , , ,  => =>
vertex is at ( , , )=( )=( , , )->Q II )->Q II
focus is at: ( , ,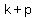 )=( )=( , ,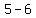 )=( )=( , , )->Q III )->Q III
=>focus and vertex lie in 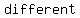 quadrants quadrants
parabola whose focus and vertex lie in different quadrant: b,c,e, and f
Answer by MathTherapy(10555)   (Show Source): (Show Source):
|
|
|