Question 1180052: The half-life of the substance is 10 years. If we begin with 20 g of the substance, how much will be left after 5 years?
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is a good question to check if a person knows the subject.
@mananth gave you INCORRECT answer, so he definitely did not pass the test.
See my correct solution below.
Since we are given that the half-life is of 10 years, we can write the decay equation in this form
m(t) =  ,
where t is the time in years; m(t) is the remaining mass; 20 is the starting mass of 20 grams.
To answer the problem's question, substitute t = 5 into the formula. Yoiu will get
m(5) = ,
where t is the time in years; m(t) is the remaining mass; 20 is the starting mass of 20 grams.
To answer the problem's question, substitute t = 5 into the formula. Yoiu will get
m(5) =  = =  = = 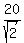 = =  = =  = 10*1.414.. = 14.14 grams (rounded).
ANSWER. 14.14 grams remained after 5 years. = 10*1.414.. = 14.14 grams (rounded).
ANSWER. 14.14 grams remained after 5 years.
Solved (correctly).
--------------
Again, if a person does not know the subject firmly or is in hurry to answer the question,
he (or she) can easily make a FATAL MISTAKE answering such question.
A dose of accuracy and expert knowledge is required . . .
///////////
On radioactive decay, see the lesson
- Radioactive decay problems
in this site.
You will find many similar (and different) solved problems there.
Use this lesson as your handbook, textbook, guide, tutorials, and (free of charge) home teacher.
Learn the subject from there once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Logarithms".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|