Question 1180041: For each equation identify the direction of opening; step pattern (a * 1,3,5) and the transformations required to get this new parabola from the original y = x2.
y = x2
y = 2(x - 1)2
y = 2(x - 1)2 + 3
y = -2(x - 3)2 - 1
y = (x + 1)2
y = (x + 3)2 - 1
please answer for every question so i can check my work thank you.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!  -> the direction of opening: opens -> the direction of opening: opens  , step pattern is ( , step pattern is ( , , , , ) )
 ->the direction of opening: opens ->the direction of opening: opens  , the vertex is ( , the vertex is ( , , ), step pattern is ), step pattern is  ( ( , , , , ) =( ) =( , , , , ) )
 ->the direction of opening: opens ->the direction of opening: opens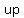 , the vertex is ( , the vertex is ( , , ), step pattern is ), step pattern is  ( ( , , , , ) =( ) =( , , , , ) )
 ->the direction of opening: opens ->the direction of opening: opens  , the vertex is ( , the vertex is ( , , ), step pattern is ), step pattern is  ( ( , , , , ) =( ) =( , ,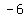 , , ) )
 ->the direction of opening: opens ->the direction of opening: opens  , the vertex is ( , the vertex is ( , , ), step pattern is ), step pattern is  ( ( , , , , ) =( ) =( , , , , ) )
 -> the direction of opening: opens -> the direction of opening: opens  , the vertex is ( , the vertex is ( , , ), step pattern is ), step pattern is  ( ( , , , , ) =( ) =( , , , , ) )
|
|
|