Question 117998: Hi, I am from Mumbai India. The problem is from " A New Approach to Mathematics & Statistics" It does not have a ISBN code.
Prove without expanding, that the following two 3x3 determinants are equal.
First determinant
(b+c-a),a,a
b,(c+a-b),b
c,c,(a+b-c)
Second determinant
a,b,c
b,c,a
c,a,b
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, I am from Mumbai India. The problem is from " A New Approach to Mathematics & Statistics" It does not have a ISBN code.
Prove without expanding, that the following two 3x3 determinants are equal.
First determinant
(b+c-a),a,a
b,(c+a-b),b
c,c,(a+b-c)
Second determinant
a,b,c
b,c,a
c,a,b
| |
|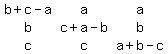 |
| | |
| |
|
|
|