Question 1179806: An insurance salesman has determined that the probability he makes a sale at a given meeting is 0.38. Assume that sales meetings are independent of each other and find the following. Use the normal approximation when appropriate.
a) What is the probabilty he makes at least one sale in 6 meetings?
.021584
b) Assuming the salesman has 6 meetings a day, 5 days a week, for 9 weeks. What is the probability he makes at least 45 sales in these 45 days?
c) Assuming that the salesman has 6 meetings a day, 5 days a week, for 9 weeks, what is the probability he makes at least one sale on each of the 45 consecutive days?
Answer by ikleyn(52870)   (Show Source):
You can put this solution on YOUR website! .
An insurance salesman has determined that the probability he makes a sale at a given meeting is 0.38.
Assume that sales meetings are independent of each other and find the following.
Use the normal approximation when appropriate.
a) What is the probability he makes at least one sale in 6 meetings?
b) Assuming the salesman has 6 meetings a day, 5 days a week, for 9 weeks.
What is the probability he makes at least 45 sales in these 45 days?
c) Assuming that the salesman has 6 meetings a day, 5 days a week, for 9 weeks,
what is the probability he makes at least one sale on each of the 45 consecutive days?
~~~~~~~~~~~~~~~~~
In this post, I provide solutions for parts (a) and (c).
(a) The event "he makes at least one sale in 6 meetings" is the COMPLEMENTARY
to the event "he makes no one sale in 6 meetings"
For this complementary event. the probability is Q = 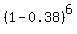 = 0.0568.
Hence, for the basic event under the problem's question, the probability is
P = 1 - Q = 1 - 0.0568 = 0.9432. ANSWER
(c) In part (a), we found out that the probability that the salesman makes at least one sail
per day is 0.9432.
Then the probability that he will make at least one sale on each of the 45 consecutive days is
 = 0.071972. ANSWER
Solved.
---------------
In this site, there are several introductory lessons on solving similar problems.
Reading these lesson can significantly help you to develop your skills and knowledge.
If you want to get links to these lessons, let me know.
|
|
|
