Question 1179804: in a block of flats there are 24 units of 3 types: the luxury unit, the superior unit and deluxe unit. the luxury can accommodate 8 people, the superior unit can accommodate 7 people and deluxe can accommodate 5 people. given that the total number of people living in this block is 160. How many of each type are there?
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39630)   (Show Source):
Answer by ikleyn(52879)  (Show Source):
You can put this solution on YOUR website! .
in a block of flats there are 24 units of 3 types: the luxury unit, the superior unit and deluxe unit.
The luxury can accommodate 8 people, the superior unit can accommodate 7 people and deluxe can accommodate 5 people.
Given that the total number of people living in this block is 160, how many of each type are there?
~~~~~~~~~~~~~~~~~~
Let x be the number of the luxury units;
y be the number of the superior units.
Then the number of the deluxe units is 24 - x - y.
Assuming maximum accommodation (fulfillment) of the units, we write this equation
8x + 7y + 5*(24-x-y) = 160.
We simplify it
8x + 7y + 120 - 5x - 5y = 160
3x + 2y = 160 - 120
3x + 2y = 40
x =  .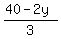
We want have x and y as integer numbers. It gives for x and y these values (see the TABLE)
T A B L E
x y z
luxury superior deluxe
---------------------------
12 2 10
10 5 9
8 8 8
6 11 7
4 14 6
2 17 5
0 20 4
In parallel, we fill the column for z = 24 - x - y.
We do it until we have non-negative values for x, y, and z.
This list in the table is the FULL SET of all possible solutions to the given problem. ANSWER
Solved.
-----------------
After reading my solution, do not forget to post your "THANKS" to me for my teaching.
It is a Math Olympiad level, or a Math circle level problem.
So, feel yourself as if you visited a Math circle session today, and as if I was your mentor.
Come again to the forum soon to learn something new (!)
Answer by greenestamps(13209)  (Show Source):
|
|
|
